The limit of envelope equation passing from the ellipse/hyperbola to parabola

Question

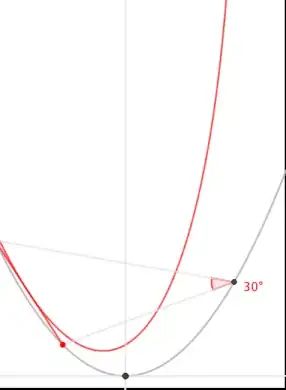
Proposition. Point $A(x_0, y_0)$ is a fixed point on the conic $C_1:ax^2 + by^2 = 1$ ($ab \neq 0$). Points $B$ and $C$ are moving on $C_1$, such that $\tan\angle BAC = t$. Then the envelope of the line $BC$ is $C_2:$ $$4ab(t^2+1)(ax^2+by^2-1) + t^2((a-b)(a x x_0 - b y y_0) + a + b)^2 = 0.\tag1\label1$$

I try to find the limit of $C_2$ when $C_1$ is a parabola $x^2=2py$.

Substituting$$y\gets y-\frac{\sqrt{a p^2+1}}{a p},\\b\gets\frac{a^2 p^2}{a p^2+1}\tag2\label2$$into the equation $C_1:a x^2+b y^2-1=0$ and taking the limit $a\to0$, $$\lim_{a\to0}\frac{ax^2+\frac{a^2 p^2}{a p^2+1}(y-\frac{\sqrt{a p^2+1}}{a p})^2-1}a=x^2-2py$$ I get the limit of $C_1$ is a parabola $\overline{C_1}:x^2=2py$.

Similarly substituting \eqref{2} and $y_0\gets y_0-\frac{\sqrt{a p^2+1}}{a p}$ into \eqref{1} and taking the limit $a\to0$, $$\lim_{a\to0}\frac{4a\frac{a^2 p^2}{a p^2+1}(t^2+1)\left(ax^2+\frac{a^2 p^2}{a p^2+1}(y-\frac{\sqrt{a p^2+1}}{a p})^2-1\right) + t^2\left((a-\frac{a^2 p^2}{a p^2+1})\left(a x x_0 -\frac{a^2 p^2}{a p^2+1} (y-\frac{\sqrt{a p^2+1}}{a p})(y_0-\frac{\sqrt{a p^2+1}}{a p})\right) + a + \frac{a^2 p^2}{a p^2+1}\right)^2}{a^4}=4 p^2 \left(t^2+1\right) \left(x^2-2 p y\right)+t^2 \left(2 p^2+p (y+y_0)+x x_0\right)^2$$ I get the limit of $C_2$ is $\overline{C_2}:4 p^2 \left(t^2+1\right) \left(x^2-2 p y\right)+t^2 \left(2 p^2+p (y+y_0)+x x_0\right)^2=0$

Is the proposition still true in the limit? That is,

Proposition. Point $A(x_0, y_0)$ is a fixed point on the conic $\overline{C_1}:x^2 =2py$. Points $B$ and $C$ are moving on $\overline{C_1}$, such that $\tan\angle BAC = t$. Then the envelope of the line $BC$ is $\overline{C_2}:$ $$\overline{C_2}:4 p^2 \left(t^2+1\right) \left(x^2-2 p y\right)+t^2 \left(2 p^2+p (y+y_0)+x x_0\right)^2=0$$

Answer 1

Working with a more form of the conic that remains well-behaved when transitioning from ellipse to parabola to hyperbola allows us to avoid taking limits.

For instance, the vertex-at-origin conic of eccentricity $e$ with semi-latus rectum $p$ (and closest focus on the positive $y$ axis) has equation $$x^2 + y^2(1-e^2)- 2p y = 0 \tag{1}$$ (Sanity check: This clearly works for the circle ($e=0$) of radius $p$. Conveniently, this matches OP's desired form for the parabola ($e=1$), albeit not OP's standard-ish form of the general conic (which has its center at the origin).)

As eccentricity crosses the parabolic threshold, the distinguished vertex remains anchored at the origin, while the other goes racing to and through infinity to "wrap around" to the underside of the $x$-axis. The parabola is a special case, but not a particularly exotic one requiring limit considerations.

Then, given fixed point $A=(x_0,y_0)$ on the conic, the envelope of chords $BC$ subtending angle $\theta$ at $A$ is given by $$4 p^2 \left(x^2 + y^2 (1 - e^2) - 2 p y \right) \;+\; \sin^2\theta\,\left(\, e^2 \left(\,xx_0 - yy_0(1-e^2) + p (y + y_0)\,\right) + 2 p^2 \,\right)^2 \;=\; 0 \tag{2}$$ Checking that this matches OP's result for origin-centered ellipses and hyperbolas is left as an exercise to the reader. For the case of the parabola, "all we have to do" is substitute $e=1$: $$4 p^2 \left(x^2 - 2 p y \right) \;+\; \sin^2\theta\,\left( \,xx_0 + p (y + y_0) + 2 p^2 \,\right)^2 \;=\; 0 \tag{2'}$$ As my $\theta$ matches OP's $\angle BAC$, so that OP's $t$ corresponds to $\tan\theta$, whence $t^2+1=\sec^2\theta$, dividing $(2')$ through by $\cos^2\theta$ verifies OP's proposition. $\square$

I'll close with a couple of GeoGebra animations, showing an ellipse and a parabola: