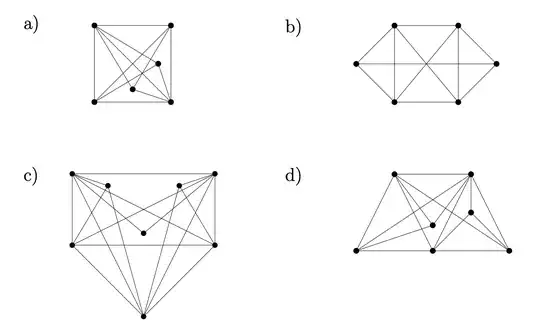
I am looking for general advice on how to find graph minors (for example $K_{3,3}$ or $K_{5}$) efficiently. I often struggle applying the Kuratowski-Wagner theorem for non-planarity, but want to improve for my upcoming exam.
As for how I currently go about determining planarity, I first spend a few minutes trying to redraw the graphs in a planar way. I move around the vertices that seems to be complicating things (for example in question A below, I might move the two vertices in the square to the outside), but doing so with pen and paper could be quite tedious, and I don't get so many tries under strict time conditions.
If that fails, I move on to finding $K_{3,3}$ or $K_5$ minors. I check if any vertex has degree less than $4$ because if there is, I only need to look for $K_{3,3}$ minors. This actually happens to be the case for all 4 example problems below. However, from here I don't really have a strategy other than just aimlessly applying edge contractions, edge deletions, and vertex deletions. I know that in each step I can't create a vertex of degree less than $2$, but other than that I feel like I just rely on luck.
What are some tips or things you guys keep in mind when trying to find graph minors that could help me out?
Any advice is welcome. Thank you.