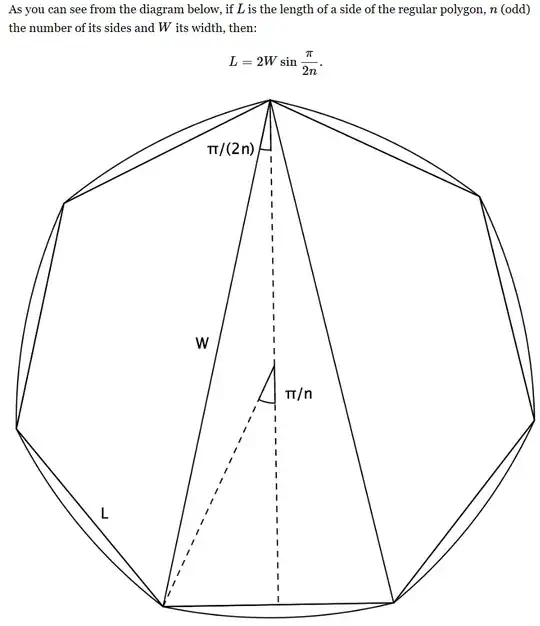
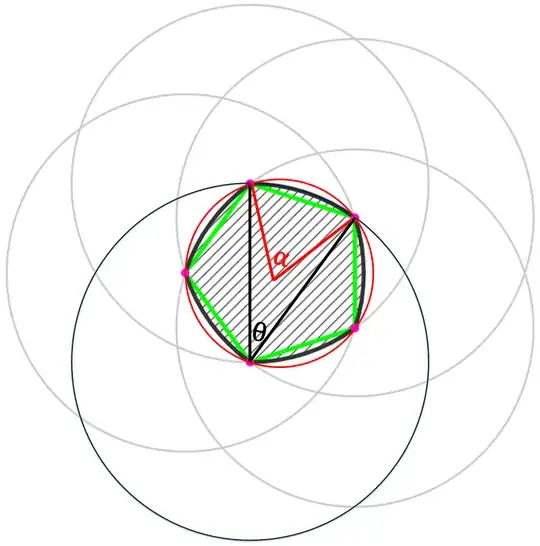
While figuring out the perimeter and area formulas for Reuleaux polygons I found the following post:
Formula to create a Reuleaux polygon
with the following answer:
Constructing the corresponding circles,
I wanted to verify that, given the (green) side length of the standard polygon, we can find each arc length of the perimeter and the area of each circular segment around the standard polygon using the Inscribed Angle Theorem ($\alpha = 2\theta$), even though $\alpha$ corresponds to the red arc and $\theta$ corresponds to the black arc. Does the Inscribed Angle Theorem work because the red and black arcs contain the same two endpoints intercepted by the arms of the red and black angles?