A line through one of the vertices of a triangle is "special" if it cuts this triangle into equal perimeters. Prove that the special lines of triangle $\triangle ABC$ meet at one point.
This is true if they also cut the area in half. This is because all of the lines would intersect the incenter and so would all meet at the incenter. Is there a way to modify this proof for any area?
Let $BC = a$, $AC = b$, $AB=c$.
The special line through $A$ meets $BC$ at $D$.
Perimeter of $\triangle ABD = AB + BD + DA = c + BD + AD$.
Perimeter of $\triangle ADC = AD + DC + CA = AD + DC + b$
Since the lines bisect the perimeter, we have,
$c+BD = BC + b$
Also, $BC=a=BD + DC$. So, let $BD=x$
We can write $DC = a-x$
$c+x=(a-x)+b$
$x=\dfrac{a+b-c}{2}$
We can also write $BD = \dfrac{a+b-c}{2}$ and $DC = \dfrac{a-b+c}{2}$.
Special line through $B$ touches $AC$ at $E$.
Perimeter of $\triangle ABE = AB + BE + EA = c + BE + EA$
Perimeter of $\triangle BCE = BC + CE + EB = a + CE + BE$
$c + AE = a + CE$.
Let $AE=y$, so, $CE=b-y$.
$c+y=a+b-y$
$y = \dfrac{a+b-c}{2}$.
So, $AE = \dfrac{a+b-c}{2}$, $CE = \dfrac{b+c-a}{2}$
Following this procedure, we have,
$AF = \dfrac{a+c-b}{2}$, $FB = \dfrac{c+b-a}{2}$
From Ceva's theorem we can prove that these lines are concurrent if, $\dfrac{BD}{Dc}. \dfrac{CE}{EA}. \dfrac{AF}{FB} = 1$.
The LHS is $$ \dfrac{a+b-c}{a-b+c}.\dfrac{b+c-a}{a+b-c}.\dfrac{a+c-b}{c+b-a} $$ You should be able to notice that every term has it's pair and indeed the left-hand side evaluates out to $1$.
Thus, it is evident that these "special lines" are concurrent
However, your proof is not clear to me. It doesn't seem the area also has to be bisected by these special lines. A median bisects the area into two and they meet at the centroid. However, it is true that the lines meet at the incentre.
Let the incircle of $\triangle ABC$ meet the sides at points $A'$, $B'$, $C'$ (with $A$ opposite $A'$, etc). Tangent segments being congruent, we can define lengths $a$, $b$, $c$ where $$a := |AB'|=|AC'| \qquad b := |BC'| = |BA'| \qquad c := |CA'| = |CB'|$$
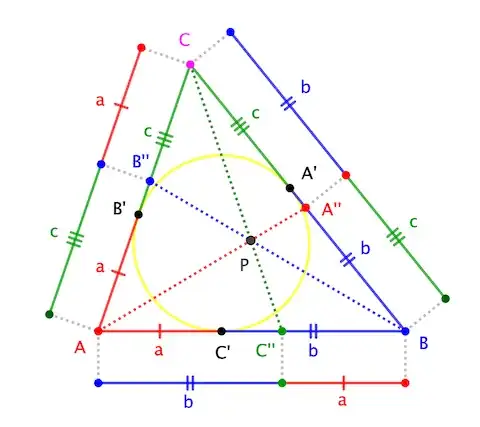
Swapping the sub-segments on each side determines points $A''$, $B''$, $C''$ such that paths along the boundary from $A$ to $A''$, from $B$ to $B''$, and from $C$ to $C''$ each has length $a+b+c$: the new points are the desired perimeter-bisecting points.
Invoking Ceva's Theorem, we find
$$\frac{|A''C|}{|BA''|} \cdot \frac{|B''A|}{|CB''|} \cdot \frac{|C''B|}{|AC''|} = \frac{c}{b} \cdot \frac{a}{c} \cdot \frac{b}{a} = 1$$
guaranteeing that cevians $AA''$, $BB''$, $CC''$ meet at a point. $\square$
Note. The argument is effectively the same as that of @RandomMathEnthusiast. RME's values $\frac12(-a+b+c)$, $\frac12(a-b+c)$, $\frac12(a+b-c)$ are precisely the lengths of the incircle-tangent segments when the sides of the triangle are $a$, $b$, $c$, but obtained algebraically.
Note 2. YNK notes in a comment to the question that $A''$, $B''$, $C''$ are points of tangency with the triangle's excircles. This old answer of mine provides a justification of this fact.
Note 3. YNK indicates in a comment this answer that the point of concurrence is the Nagel point, indexed as $X_8$ in the Encyclopedia of Triangle Centers.
As it happens, cevians $AA'$, $BB'$, $CC'$ also concur, at the Gergonne point, aka $X_7$ in the ETC.
The fact that $A'$ and $A''$ (likewise, $B'$ and $B''$, and $C'$ and $C''$) are mutual reflections in the midpoint of the side of the triangle makes $X_7$ and $X_8$ "isotomic conjugates".