Construction of the orthic inellipse

Question

A triangle ABC with A(0,0), B(6,0) and C(1,5). Let's consider the three altitudes (A,Ha), (B,Hb) and (C,Hc). K is the symmedian point, the center of the orthic inellipse. I'm looking for the radii of orthic inellipse. I've found (I think) the general equation of the ellipse

$x^2 - 0.8889xy + 0.8889y^2 - 2x -1.3333y + 1 = 0$

I think I've also got the right angle for the main axis: $\alpha =0.84757$, but I can't find $a$ and $b$ the radii.

Here's what I tried:

1. formules from wikipedia $A = a^2\sin^2(\alpha)+b^2\cos^2(\alpha)$ and $C = a^2\cos^2(\alpha)+b^2\sin^2(\alpha)$

With these formulas, I find $a=1.18$ which is wrong because $KHa\approx 1.89$.

2. I also tried to find the coordinates of Ha and Hb in the reference frame (k,KP,KQ). As the equation of the ellipse is written $x^2/a^2 +y^2/b^2 = 1$, I thought I'd have a way of finding $a$ and $b$ easily. Always a bad result.

update

If $m = (xHa)^2$, $n=(yHa)^2$, $p = (xHb)^2$, $q=(yHb)^2$ then $a = \sqrt{(m * q - n * p) / (q - n)}$. I had forgotten to square the coordinates. I believe this is the simplest solution to avoid the complexity of calculations and formulas.

3. Finally, I get the right result using the following formulas:

Values update( I didn't display the right ones)

$a =1.8963929229511;b= 1.1324841775466$

But where does the error come from with the first methods?

Am I applying formulas that don't fit the context?

I gave geogebra a try to check my equation

Answer 1

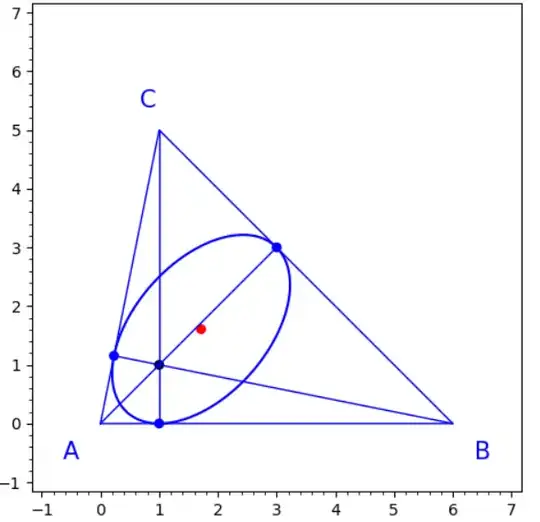
Fig. 1 : The center $\Gamma$ of the ellipse is featured in red. The blue cevians are the altitudes $AA',BB',CC'$.

First of all, I re-write the equation of your ellipse with integral coefficients :

$$9x^2+8y^2-8xy-18x-12y+9=0\tag{1}$$

I disagree with the values of the semi-axes you have found.

I find them to be, approximately :

$$\begin{cases}a \approx 1.8963929229510588848213517082\\ b \approx 1.1324841775465934243225444517\end{cases}\tag{2}$$

Here is a sanity check for the value of $a$:

• the foot $A'$ of the altitude issued from $A$ has coordinates $(3,3)$ (easy checking).

• The coordinates $(\tfrac{48}{28},\tfrac{45}{28})$ of the center $\Gamma$ of the ellipse aren't difficult to find (see (4) below).

Line segment $[\Gamma A']$ is visibly almost a main semi-axis. Therefore the distance $d(\Gamma,A')\approx 1.89555...$ should and is indeed very close to the value of $a$ given in (2).

How these values of $a,b$ been found ? Classically,

1. First of all, by computing the coordinates of the ellipse's center. This is done by setting the partial derivatives of (1) to $0$ :

$$\begin{cases} \ \ 18x-8y&=&16\\-8x+16y&=&12\end{cases},\tag{3}$$

a linear system with solution:

$$(x_0=\tfrac{48}{28}, \ \ y_0=\tfrac{45}{28})\tag{4}$$

2. Then, setting $x=x_0+X, \ y=y_0+Y$ in (1) gives rise to the reduced form

$$9X^2-8XY+8Y^2=\underbrace{\frac{225}{14}}_{= c},\tag{5}$$

Otherwise said :

$$\pmatrix{X &Y}\underbrace{\pmatrix{ \ \ 9&-4\\-4& \ \ 8}}_M\pmatrix{X\\Y}=c\tag{6}$$

3. Last step : Let $\lambda_k=\tfrac12(17 \pm \sqrt{65})$ be the eigenvalues of $M$ ; then formulas

$$a,b=\sqrt{\frac{c}{\lambda_k}}$$

give semi-axes lengths whose numerical values have been given in (2).

---

Appendix (I will expand it tomorrow ; it is too late at present : midnight CET).

In fact, I have computed (1) by using barycentric coordinates $(p:q:r)$ and barycentric equations with these coordinates.

It is known (see here) that he barycentric equation of an ellipse internaly tangent to a triangle is :

$$p^2l^2+q^2m^2+r^2n^2-2(pqlm+qrmn+prnl) = 0\tag{7}$$

where $l,m,n$ parameters such that the (un-normalized) barycentric coordinates of the Darboux point are : $(1/l:1/m:1/n)$

In the present case, the Darboux point is the orthocenter whose barycentric coordinates are

$$(\tfrac{1}{2S_A}:\tfrac{1}{2S_B}:\tfrac{1}{2S_C})\tag{8}$$

where $2S_A=b^2+c^2-a^2=12, \ \ 2S_B=c^2+a^2-b^2=60, \ \ 2S_C=a^2+b^2-c^2=40\tag{9}$

using Conway's notations where $a=5 \sqrt{2},b=\sqrt{26},c=6$ are the side lengths of the triangle ; the resulting barycentric equation of the ellipse is :

$$36p^2+900q^2+400r^2-2(180pq+600qr+120rp)=0\tag{8}$$

Switching from barycentric coordinates to cartesian coordinates is done by plugging formulas :

$$p=-(x+y)/3+2,\ \ q=(5x-y)/15, \ \ r=2y/5$$

in (8), finally giving (1).

---

Here is the Sage program (running it is very easy : just type the word sagecell and press "Enter". An edit window is opened. Copy-paste this program, then press button "execute") :

 var('p q r p0 q0 r0 x y X Y')
 M=matrix(
      [[0,6,1],
      [0,0,5],
      [1,1,1]]) ; # direct matrix containing coord. of A,B,C
 N=M^(-1) ; # its inverse matrix
 print(N)
 #The value of N is copied here for further reference :
 N=matrix([[-1/3,-1/3,2],
 [  1/3,-1/15,0],
 [    0,2/5,0]])
 V=matrix([[x],[y],[1]])
 W=N*V;# W contains bar. coord corresponding to cart. coordinates (x,y)
 p0=W[0][0];q0==W[1][0];r0==W[2][0]
 # barycentric equation :
 e=36*p^2+900*q^2+400*r^2-2*(180*p*q+600*q*r+120*r*p)
 # conversion into cartesian equation 
 #e=e.subs(p==(-(x+y)/3+2),q==(5*x-y)/15,r=2*y/5)
 e=e.subs(p==p0,q==q0,r==r0)
 #LHS of barycentric equation :
 e=36*p^2+900*q^2+400*r^2-2*(180*p*q+600*q*r+120*r*p) :
 e=e.expand().full_simplify()
 e=e/16
 eq=e.subs(x==X+48/28,y==Y+45/28)
 eq=eq.expand()
 show(eq)
 dx=x-48/28;dy=y-45/28;
 eq=9*dx^2+8*dy^2-8*dx*dy
 eq=eq.expand()
 show(eq)
 ss=solve(x^2-17*x+56==0,x)
 show(ss)
 a=(1/sqrt((ss[0].rhs())*(14/225))).n(100)
 print(a)
 b=(1/sqrt((ss[1].rhs())*(14/225))).n(100)
 print(b)
 g=implicit_plot(e,(x,-1,7),(y,-1,7))
 g+=line(((0,0),(6,0),(1,5),(0,0)))
 g+=line(((0,0),(3,3)),color='blue')
 g+=line(((1,5),(1,0)),color='blue');g+=point((48/28,45/28),pointsize=30,color='red');g+=point((3,3),pointsize=30,color='red');g+=point((1,1),pointsize=30,color='green')
 g+=text('A', (-0.5,-0.5),fontsize=15)
 g+=text('B', (6.5,-0.5),fontsize=15)
 g+=text('C', (0.8,5.5),fontsize=15)
 show(g)

Answer 2

The first formulas you used are meant to provide a possible set of coefficients $A$, $B$, ..., $F$ of the general equation, given $a$, $b$, rotation angle $\alpha$ and center $(x_0,y_0)$. But bear in mind that you can multiply those coefficients by an arbitrary constant $k\ne0$ and get the same ellipse.

To invert those formulas and get $a$, $b$, $\alpha$, $x_0$, $y_0$ from the general coefficients, you must take into account all the equations and also insert $k$ as an unknown:

$$ {\displaystyle {\begin{aligned} kA&=a^{2}\sin ^{2}\alpha +b^{2}\cos ^{2}\alpha \\ kB&=2\left(b^{2}-a^{2}\right)\sin \alpha \cos \alpha \\ kC&=a^{2}\cos ^{2}\alpha +b^{2}\sin ^{2}\alpha \end{aligned}}} $$

That way you can obtain the inverse formulas that you successfully used.