1

Let us take the construction for the Triangle triple product identity and move the segments on each side in a circular order clockwise, or counter clockwise, as shown in the diagram:

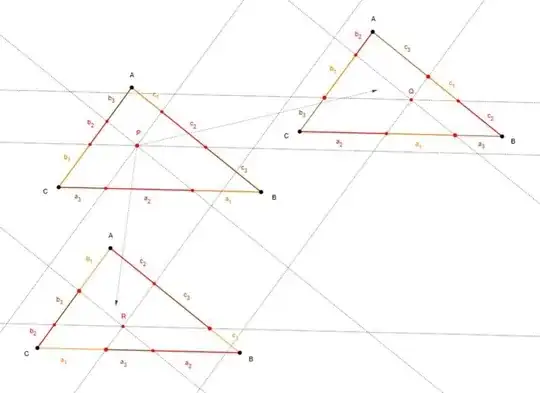
Triangle triple product identity symmetry

I am trying to prove the following statements:

  1. The lines connecting the new segments endpoints are also parallel to the sides of $ABC$, and intersect at one point for each permutation direction (the points $Q$ and $R$ on the diagram).
  2. The centroids of the triangles $ABC$ and $PQR$ coincide.

The construction works for the points outside of $ABC$ as well.

Alex C
  • 1,238

1 Answers1

1

If the barycentric coordinates of $P$ are $u:v:w$, then one readily shows that $$a_2:a_3:a_1\;=\; b_1:b_2:b_3\;=\;c_3:c_1:c_2 \;=\; u:v:w \tag1$$ The parallelism property is equivalent (by similar triangles) to the fact that the non-middle sub-segments corresponding to the same coordinate are adjacent to a common side of the triangle.

For instance, $b_1$ and $c_3$ (the "$u$" sub-segments) are adjacent to side $a$, and they determine (and are determined by) a parallel to $a$ precisely because $$\frac{b_1}{b}=\frac{c_3}{c}\quad\left(=\frac{u}{u+v+w}\right) \tag2$$

Cyclically permuting the segments along the sides, we have in the $Q$ triangle that the "$w$" sub-segments $b_3$ and $c_2$ are adjacent to side $a$, etc; in the $R$ triangle, the "$v$" sub-segments $b_2$ and $c_1$ are, etc; thus, the segments determine parallels to the sides. Moreover, the process merely permutes the barycentric coords of the points of $P$, so that $Q$ and $R$ have coords $v:w:u$ and $w:u:v$ (and must be the points of concurrence of the respective parallels), and the centroid property easily follows. $\square$

Note on Notation. It may help in keeping subscripts straight to adjust the notation to better reflect the geometry.

For instance, along side $a$, rename $a_1$ to $a_C$, since its length is determined by the parallel to side $c$; likewise, rename $a_3$ to $a_B$; then middle sub-segment $a_2$ becomes $a_A$ by default. Further, change $$b_1\to b_A \quad b_2\to b_B \quad b_3\to b_C \qquad c_3\to c_A \quad c_1\to c_B \quad c_2\to c_C$$ With this notation, relations $(1)$ and $(2)$ become more visually symmetric, especially if we also rename coordinates $u$, $v$, $w$, to, say, $x_A$, $x_B$, $x_C$ and define $x:=x_A+x_B+x_C$: $$a_A:a_B:a_C\;=\; b_A:b_B:b_C\;=\;c_A:c_B:c_C \;=\; x_A:x_B:x_C \tag{1'}$$ $$\left(\frac{a_A}{a}=\right)\quad\frac{b_A}{b}=\frac{c_A}{c}\quad\left(=\frac{x_A}{x}\right) \tag{2'}$$ So, sub-segments with the same subscript are proportional with their sides. Further, in the discussion of the cyclic permutation, we observe that sub-segments adjacent to a given side have the same subscript (eg, in the $Q$ triangle, $b_C$ and $c_C$ are adjacent to side $a$), and hence are proportional, implying the parallelism property (and thus also the centroid property).

Blue
  • 83,939