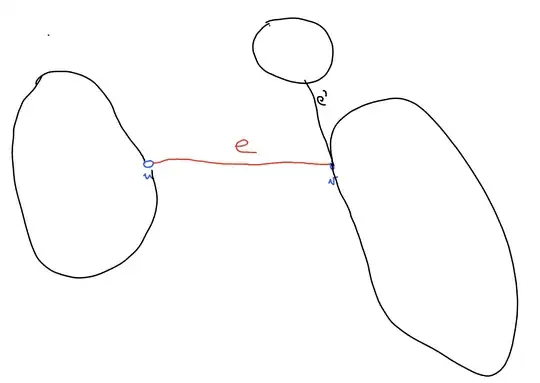
Let $G = (V, E)$ be a graph, and let $e \in E$ be a cut edge. Show that the removal of $e$ increases the number of connected components by exactly $1$

Question

Let $G = (V, E)$ be a graph, and let $e \in E$ be a cut edge. Show that the removal of $e$ increases the number of connected components by exactly $1$, i.e.,

$$ c(G - e) - c(G) = 1. $$

---

My Proof:

Suppose $e = \{u,v\} \in E$ and that it is a cut edge. By definition, a cut edge is an edge whose removal increases the number of connected components.

Thus, removing $e$ from $G$ results in a graph $G - e$ where $u$ and $v$ are no longer connected, leading to the formation of two distinct connected components where there was previously one. This implies that the number of connected components strictly increases, giving:

$$ c(G - e) > c(G). $$

Now, consider the graph $G - e$. If we add back the edge $e$, the two disconnected components merge into a single connected component, decreasing the total count by exactly $1$. That is,

$$ c(G) = c(G - e) - 1. $$

Rearranging, we obtain the desired result:

$$ c(G - e) - c(G) = 1. $$

---

Is this proof sufficiently rigorous? Can someone make it even more formal? I want to avoid any loose terminology and ensure that the argument is mathematically precise.

Answer 1

I do not see any issue in your solution, or your writing.

I'd solve it in this way:
Let's prove it by contradiction, assume after the removal of $e = (u, v)$, 3 vertices $w_1, w_2, w_3$ got disconnected(no pair of them are connected).
Let $p_1 \colon= \text {shortest path from } w_1 \text{ to } w_3$,
$p_2 \colon= \text {shortest path from } w_2 \text{ to } w_3$ and
$p_3 \colon= \text {shortest path from } w_1 \text{ to } w_2$.

Since these vertices got disconnected because of the removal of $e$ their path in $G$ must pass through $e$, then by the pigeonhole principle, at least 2 of these paths pass through $v$ before $u$. We will show in all of 3 cases, 2 of them will still be connected in $G - e$ which is a contradiction.
if the paths were $p_1$ and $p_2$:
$p_1 =$ $<w_1, \cdots, v, u, \cdots, w_3>$, $p_2 =$ $<w_2, \cdots, v, u, \cdots, w_3>$, and we know path from $w_1$ and $w_2$ to $v$ doesn't pass through $e$ because of the assumption that these are shortest paths. so $w_1$ and $w_2$ are connected to $v$, and because of transitive of connection in undirected graphs, we have $w_1$ and $w_2$ are connected; contradiction.

for $p_1, p_3$, by the same reasoning $w_2$ and $w_3$ are connected to $u$ thus connected which is a contradiction.

for $p_2, p_3$:
for $p_2$ and $p_3$ to pass through $v$, it means that there is an edge from the connected component of $u$ to the connected component of $v$ in $G - e$ which contradicts $e$ being a bridge.

Answer 2

I would likely approach this using a proof by contradiction.

Here is my approach:

Let $G = (V, E)$ be a graph, and let $e \in E$ be a bridge. Assume that removing $e$ does not increase the number of connected components by exactly 1. This means one of the following two cases must hold:

1. The number of components does not increase at all.
2. The number of components increases by at least 2.

Case 1: The number of components does not increase.

By definition, a cut edge is an edge whose removal increases the number of connected components. However, in this case, removing $e$ does not change the number of components, which contradicts the assumption that $e$ is a cut edge. Thus, this case is impossible.

Case 2: The number of components increases by at least 2.

This would imply that removing $e$ separates $G$ into at least three connected components. However, since $e$ is an edge, it connects exactly two vertices in $G$, meaning that removing it can only separate one component into at most two new components. Therefore, this contradicts our assumption, and this case is also impossible since $u$ and $v$ have to be in different components.

Since both cases lead to contradictions, our assumption must be false. Therefore, removing a cut edge must increase the number of connected components by exactly 1.