10

Show that $$I=\int_0^{\pi/6}\arccos\left(\frac{\sin x}{\cos 2x}\right)dx=\frac{\pi^2}{16}.$$

Wolfram suggests that it's true, but does not evaluate the indefinite integral.

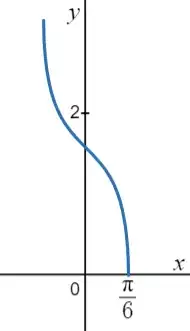
Here is the graph of the integrand.

enter image description here

Substituting $\sin x\to x$, we get

$$I=\int_{0}^{1/2}\frac{1}{\sqrt{1-x^{2}}}\arccos\left(\frac{x}{1-2x^{2}}\right)dx$$

I don't know what to do with this.

Context: This integral is part of my answer to a probability question about a triangle whose vertices are three random points on a cirlce. I have encountered integrals involving arccos related to other geometric probability questions (example1, example2, example3), and they are beyond my integration skills.

user170231
  • 25,320
Dan
  • 35,053
  • 2
    1 iteration of IBP gives $$\frac{\pi^2}{4} + \int_0^{\frac{1}{2}} \frac{ \arccos t}{ \sqrt{(1-2t^2)^2 - t^2}} \left(1 - \frac{2}{1-2t^2} \right) dt$$ so we are done if we show $$ \int_0^{\frac{1}{2}} \frac{ \arccos t}{ \sqrt{(1-2t^2)^2 - t^2}} \left(1 - \frac{2}{1-2t^2} \right) dt = \frac{3 \pi^2}{16}$$ It seems that $\arccos t$ however doesn't have a nice series expansion. Maybe substituting $t = \cos x$ leads to something interesting, but I half expect it to just give a shifted version of the above integral – Kraken Mar 08 '25 at 11:27
  • 1
    after much simplification the integral transforms to $\frac{1}{4}\int_{\frac{1}{2}}^{1}\frac{\cos^{-1}(t)(2-t)}{t\sqrt{(2t-1)(1-t^2)}} dt$ though I am still not able to solve this – lilychou Mar 08 '25 at 13:02
  • 3
    I am very sad to not obtain the result except using an inverse symbolic calculator at the end. This is a nice problem which received an elegant solution from @Cyankite. Cheers :-( – Claude Leibovici Mar 09 '25 at 10:11

2 Answers2

16

The strategy is similar to that of those analogous arccos integrals on this site. For a detailed description to the strategy, see the accepted answer to this question.

$$ \begin{align} I & = \int_{0}^{1/2}\frac{1}{\sqrt{1-x^{2}}}\arccos\left(\frac{x}{1-2x^{2}}\right)dx \\ & = \int_{0}^{1/2}\frac{1}{\sqrt{1-x^{2}}}\arctan\left(\frac{\sqrt{4x^4-5x^2+1}}{x}\right)dx \\ & = \int_{0}^{1/2}\frac{1}{\sqrt{1-x^{2}}}\arctan\left(\frac{\sqrt{1-x^2}}{x} \cdot \sqrt{1-4x^2}\right)dx \\ & = \int_0^{1/2} dx \int_0^{\sqrt{1-4x^2}} \frac{x}{x^2+y^2-x^2y^2} dy \\ & = \int_0^1 dy \int_0^{\sqrt{1-y^2}/2} \frac{x}{x^2+y^2-x^2y^2} dx \\ & = \int_0^1 \frac{1}{2(1-y^2)} \left( \log \left( \frac{(1-y^2)^2}{4} + y^2\right) - \log(y^2) \right) dy\\ & = \int_0^1 \frac{\log((y^2+1)/2y)}{y^2-1} dy \\ & \overset{y=\frac{1-x}{1+x}}{=} \int_0^1 \frac{\log((1+x^2)/(1-x^2))}{2x} dx \\ & = \frac12 \int_0^1 \frac{\log(1+x^2)}{x}dx - \frac12 \int_0^1 \frac{\log(1-x^2)}{x}dx \\ & = \frac 12 \frac{\pi^2}{24} + \frac12 \frac{\pi^2}{12} = \boxed{\frac{\pi^2}{16}} \end{align} $$

Dan
  • 35,053
Cyankite
  • 1,049
5

This is not an answer.

If we use the series expansion of the arc cosine function, the integral is $$I=\frac{\pi ^2}{12}-\sum_{n=0}^\infty \frac{ (2 n)! }{4^n\,(2 n+1)\, (n!)^2}\int_0^\frac \pi 6\Big(\sin (x) \,\sec (2 x)\Big)^{2 n+1}\,dx$$ According to Mathematica, the required antiderivative is given in terms of the Appell hypergeometric function of two variables and $$J_n=\int_0^\frac \pi 6\Big(\sin (x) \,\sec (2 x)\Big)^{2 n+1}\,dx$$ $$J_n=\frac {F_1\left(n+1;2 n+1,\frac{1}{2}-n;n+2;\frac{1}{3},-\frac{1}{3}\right)}{2\, 3^{n+1}\, (n+1) }$$

If $a_n$ is the summand, asymptotically $$\frac {a_{n+1}}{a_n}=1-\frac{5}{2 n}+\frac{111}{25 n^2}+O\left(\frac{1}{n^3}\right)$$ The summation converges to a number which an inverse symbolic calculator finds to be $\frac {\pi^2}{48}$. Then the result.

The funny story is that, if we compute the $J_n$ one at the time, we have a bunch of logarithms such as $$J_0=\frac{1}{4 \sqrt{2}}\log \left(833-588 \sqrt{2}-480 \sqrt{3}+340 \sqrt{6}\right)$$ $$J_1=\frac{5-3 \sqrt{3}}{16}+\frac{7}{64 \sqrt{2}}\log \left(833-588 \sqrt{2}-480 \sqrt{3}+340 \sqrt{6}\right)$$ which is normal since the tangent half-angle substitution leads to $$\int\Big(\sin (x) \,\sec (2 x)\Big)^{2 n+1}\,dx=4^{n+1}\int\frac{1}{1+t^2}\left(\frac{t \left(t^2+1\right)}{t^4-6 t^2+1}\right)^{2 n+1}\,dt$$

Claude Leibovici
  • 289,558