How to evaluate $\int_0^\infty\frac{t^{-a}-t^{-b}}{1-t}dt$ without using harmonic number or series?

Question

I am working on $$ I=\int_0^\infty\frac{(1-t^5)t^4}{1-t^{24}}dt.\tag{1} $$ After the change of variable $t\to t^{\frac1{24}}$, I have \begin{eqnarray*} I&=&\frac1{24}\int_0^\infty\frac{t^{-\frac{19}{24}}-t^{-\frac{14}{24}}}{1-t}dt \\ &=&\frac1{24}\int_0^1\frac{t^{-\frac{19}{24}}-t^{-\frac{7}{12}}}{1-t}dt+\frac1{24}\int_1^\infty\frac{t^{-\frac{19}{24}}-t^{-\frac{14}{24}}}{1-t}\overset{t\to\frac1t}{dt} \\ &=&\frac1{24}\int_0^1\frac{t^{-\frac{19}{24}}-t^{-\frac{7}{12}}}{1-t}dt+\frac1{24}\int_0^1\frac{t^{-\frac{5}{12}}-t^{-\frac{5}{24}}}{1-t}dt\\ &=&\frac1{24}\int_0^1\frac{t^{-\frac{19}{24}}-t^{-\frac{7}{12}}+t^{-\frac{5}{12}}-t^{-\frac{5}{24}}}{1-t}dt\\ &=&\frac1{24}(H_{-\frac7{12}}-H_{-\frac{5}{12}}+H_{-\frac{5}{24}}-H_{-\frac{19}{24}})\\ &=&\frac1{24}(H_{-\frac7{12}}-H_{\frac{7}{12}-1}+H_{-\frac{5}{24}}-H_{\frac{5}{24}-1})\\ &=&\frac\pi{24}(\cot(\frac7{12}\pi)+\cot(\frac5{24}\pi))\\ &=&\frac\pi{12}\sqrt{2-\sqrt3}. \end{eqnarray*} Here $$ H_{-x}-H_{x-1}=\pi\cot(\pi x)$$ is used (see https://en.wikipedia.org/wiki/Harmonic_number). Generally $$\int_0^\infty\frac{t^{-a}-t^{-b}}{1-t}dt=\pi(\cot(b\pi)-\cot(a\pi)). \tag{2}$$ Here $0<a,b<1$. I also tried series method. Now my question is: how to use elementary method to evaluate (1) or (2) without using the Harmonic number or series?

Answer 1

The integral can be evaluated by residue calculus. I will adapt below the solution of a similar problem which can be found here.

Instead of $$ J(a,b)=\int_0^\infty\frac{t^{-a}-t^{-b}}{t-1}dt $$ we will evaluate $$ I(a)={\rm p.v.} \int_0^\infty\frac{t^{-a}}{t-1}dt. $$ Then $J(a,b)=I(a)-I(b)$.

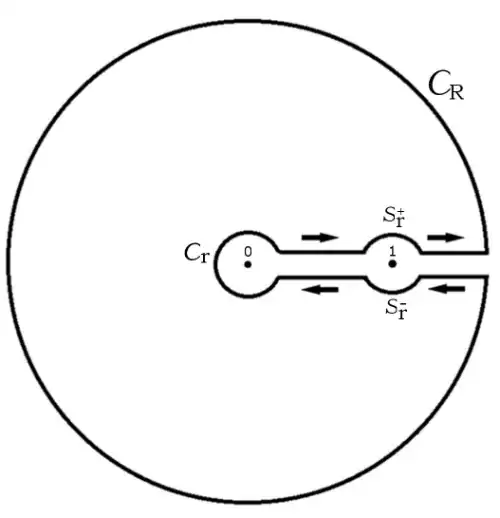
Given $0<\text{Re}(a)<1$ let $Γ$ be the following contour with the branch cut of the logarithm chosen along the positive real axis. Notice the relation $z_-=e^{2\pi i}z_+$, connecting the values of $z$ along lower and upper banks of the cut.

The integrals of the function $\displaystyle f(z)=\frac{z^{-a}}{z-1}$ on $C_r$ and $C_R$ obviously vanish as $r \to 0^+$ and $R \to \infty$, respectively. The integral over $S_r^+$ is

$$ I_ {S_r^+}=\lim_{z\to1}\int_{ S_r^+} f(z) dz=\lim_{r\to0}\int_\phi f(1+re^{i\phi}) d(1+re^{i\phi}) =i\lim_{r\to0}\int_\pi^0 (1+re^{i\phi})^{-a} d\phi=-\pi i $$ and its counterpart $I_ {S_r^-}=e^{-2\pi i a}I_ {S_r^+}$.

Further we have: $$\left(\int_R^{1+r} + \int_{1-r}^r\right)f(z)dz=-e^{-2\pi ia}\left(\int_r^{1-r} + \int_{1+r}^R\right)f(z)dz,$$ so that by residue theorem one obtains in the limit ($r\to0^+$, $R\to\infty$): $$ (1-e^{-2\pi ia})I(a)-\pi i(1+e^{-2\pi ia})=0 $$ or $$ I(a)=\pi i\frac{1+e^{-2\pi ia}}{1-e^{-2\pi ia}}=\pi\cot(\pi a). $$

Answer 2

Well, notice that we can use the evaluating integrals over the positive real axis property of the Laplace Transform:

$$\text{f}\left(\alpha,\beta\right):=\int\limits_0^\infty\frac{x^\alpha-x^\beta}{1-x}\space\text{d}x=\int\limits_0^\infty\left(\mathscr{L}_x\left[x^\alpha\right]_{\left(\sigma\right)}-\mathscr{L}_x\left[x^\beta\right]_{\left(\sigma\right)}\right)\cdot\mathscr{L}_x^{-1}\left[\frac{1}{1-x}\right]_{\left(\sigma\right)}\space\text{d}\sigma\tag1$$