0

How do I eliminate 1 (Incorrect point) and use the remaining points to calculate the center. I currently use Nelder mead to optimize and ignore a points, but my cost function involves radius check, which is not ideal, because I want a radius agnostic solution.

Cost Function used: Radius - SQRT(XY distance between calculated center and Vertex)

Context: My goal is to find which sensor is incorrect and ignore it, as the object I'm detecting has defects on a portion of the circle, but I still want to detect the center accurately.

Edit: Readings are from a sensor - accuracy though high is ~ 0.1 mm. So it needs to be done with some tolerance.

Abhi
  • 17
  • 6
    Perhaps I am missing the point but given any three non-colinear points it's easy to find the center of the unique circle that passes through them. There are only $\binom 53=10$ ways to choose $3$ points out of your five and you should see that including one of the points gives a different center while any triple chosen from the other four yields the same center. What's wrong with that? – lulu Feb 27 '25 at 20:04
  • 1
    Please clarify your specific problem or provide additional details to highlight exactly what you need. As it's currently written, it's hard to tell exactly what you're asking. – Community Feb 27 '25 at 20:07
  • Welcome to Math.SE! ... Please describe your situation in more detail. What exactly do the sensors tell you? What exactly is your cost function? (Maybe there's a way to improve it.) It would probably help to provide an example or two; list the points your given, the sensor readings, your analysis, and the identity of the incorrect point. I'm also curious to know how the five points arise, and what guarantees that exactly four of them are definitely on a common circle. ... Add such context and clarifications to the body of the question. Comments are easily overlooked and may be hidden. – Blue Feb 27 '25 at 21:11
  • 1
    You updated the question, but you didn't respond to Lulu's suggestion above. I don't understand why it doesn't solve your problem. – MJD Feb 27 '25 at 22:07

1 Answers1

3

Given $n=3$ points with coordinates $(x_i,y_i)$ you can find the parameters $(a,b,r)$ of the circle such that $$ (x-a)^2 +(y-b)^2 = r^2 $$ is the equation of the circle.

use https://math.stackexchange.com/a/213670/3301 for one of the ways to get the center and radius of a circle from 3 points.

There are $10$ combinations to consider given that the order isn't important of which three points are to be included at a time

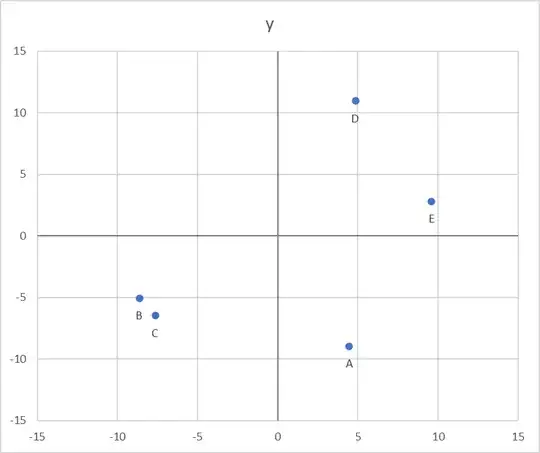
In the example below I have labeled the 5 points as $A,B,C,D,E$ and made $D$ the bad one

fig1

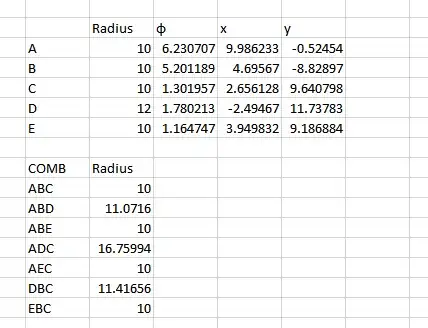
As pointed out in the comments, I only tested for 7 combinations instead of the full 10, missing the ADE, BDE, and CDE rows. The process is the same though.

As you can see, the three results that give the same result for radius do not contain the bad point. So the other three $ABD$, $ADC$ and $DBC$ above have point D in common and hence it is the bad one.

Here is the VBA function that calculates the radius of a circle from three points

Public Function CalcRadiusFromThreePoints(ByRef rng_A As Range, ByRef rng_B As Range, ByRef rng_C As Range) As Variant
    Dim A() As Variant, B() As Variant, C() As Variant, R As Variant
    Dim D As Variant, KX As Variant, KY As Variant, cx As Variant, cy As Variant
    A = rng_A.Value
    B = rng_B.Value
    C = rng_C.Value

D = A(1, 1) * (B(1, 2) - C(1, 2)) + B(1, 1) * (C(1, 2) - A(1, 2)) + C(1, 1) * (A(1, 2) - B(1, 2))


KX = (-(A(1, 1) ^ 2) + (B(1, 1) ^ 2) - (A(1, 2) ^ 2) + (B(1, 2) ^ 2)) / 2#
KY = (-(B(1, 1) ^ 2) + (C(1, 1) ^ 2) - (B(1, 2) ^ 2) + (C(1, 2) ^ 2)) / 2#


cx = -(KX * (B(1, 2) - C(1, 2)) + KY * (B(1, 2) - A(1, 2))) / D
cy = -(KX * (B(1, 1) - C(1, 1)) + KY * (B(1, 1) - A(1, 1))) / D


R = Sqr((A(1, 1) - cx) ^ 2 + (A(1, 2) - cy) ^ 2)


CalcRadiusFromThreePoints = R




End Function

and it is used with three arguments, each being a range of 1×2 cells for the (x,y) coordinates of a point.

fig2

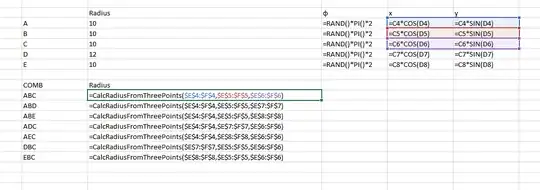
and here is an example of 5 points, of which point D has a radius of $12$, and all the other ones have a radius of $10$, and are randomly placed somewhere around the circle.

fig3

John Alexiou
  • 14,616
  • Why "There are 7 combinations to consider" and not 10? Why doesn't your list consider ADE, BDE, or CDE? – MJD Feb 27 '25 at 23:04
  • Exactly, Isn't 5C2 = 10? – Abhi Feb 27 '25 at 23:26
  • @MJD - Yeah, In my head I did the permutations and I guess I miss some. The general process is the same. Find the 3 combinations with the widely different results and look at the point that they have in common. – John Alexiou Feb 28 '25 at 00:31
  • @Abhi - the Radius and Φ columns are used to construct points on a circle. The radius is 10 for all but one point in order to meet the specifications of the question. The azimuth angle Φ is random between 0 and 2π. – John Alexiou Feb 28 '25 at 00:34
  • Do you suggest KNN after to find the 4 nearest neighbors? and use the average of the 4 as the center? – Abhi Feb 28 '25 at 00:45
  • @Abhi - not at all. The center from 3 points is calculated in the VBA routine as cx and cy variables. – John Alexiou Feb 28 '25 at 05:01