Prove that: $\vec{DZ}=\frac{1}{a+c+d}(c·\vec{DA}+ d·\vec{DC})$

Question

The problem

Consider the inscribable quadrilateral $ABCD$ with $AC=a, CD=c, DA=d$. Let the points $X$ and $Y$ be on the lines $AB$ and $BC$, respectively, such that $A\in (BX), C\in (BY) $ and $BX=BY=BD$. If the angle bisector $DAC$ intersects the line $XY$ at the point $Z$, prove that: $$ \vec{DZ}=\frac{1}{a+c+d}(c·\vec{DA}+ d·\vec{DC}) $$ My idea

(I will add a drawing later)

So when I saw what we had to demonstrate, I immediately thought of the formula that says that if we have a triangle ABC and I in the centre of the inscribed circle in that triangle, then we have $$\newcommand{\parallelsum}{\mathbin{\!/ \mkern-5mu // \!}} \vec{PI}=\frac{1}{a+b+c}(\vec{PA}·a + \vec{PC}·c + \vec{PB}·b). $$ They are kinda similar, and I think this might help.

I played with the angles, and all Ineededd to demonstrate to prove what I need is that $XA=XY$ or $AC\parallelsum XY$ (see more in the comments)

Also, when I hear about an inscribed circle, I first think of the power of the point and congruent angles.

I got to nothing by trying the power of the pint path, but the idea with congruent angles might help because we also have the triangle $BXY$ and $BYD$ isosceles. I hope one of you can help me! Thanks.

Answer 1

Let $I$ be the incenter of $\triangle{ACD}$.

As you wrote, we have $$\vec{PI}=\frac{a\vec{PD}+c\vec{PA}+d\vec{PC}}{a+c+d}$$ (A proof is written, for example, here.)

So, taking $P=D$, we get $$\vec{DI}=\frac{c\vec{DA}+d\vec{DC}}{a+c+d}$$ So, in order to prove that $\vec{DZ}=\frac{c\vec{DA}+d\vec{DC}}{a+c+d}$, it is sufficient to prove that $Z=I$. In order to prove that $Z=I$, it is sufficient to prove that $I$ is on the line $XY$.

So, in the following, let us prove that $I$ is on the line $XY$.

Let $E$ be the intersection point of $AC$ with $BD$.

There are positive real numbers $p,q$ such that $\vec{BX}=p\vec{BA},\vec{BY}=q\vec{BC}$ i.e. $$\vec{DA}=\frac 1p\vec{DX}-\frac{1-p}{p}\vec{DB}\tag1$$ $$\vec{DC}=\frac 1q\vec{DY}-\frac{1-q}{q}\vec{DB}\tag2$$ We have $|\vec{BD}|=|\vec{BX}|=|\vec{BY}|$,i.e. $|\vec{BD}|=p|\vec{BA}|=q|\vec{BC}|$. By Ptolemy's theorem, we have $AB\cdot CD+BC\cdot AD=AC\cdot BD$, i.e. $\frac{BD}{p}\cdot c+\frac{BD}{q}\cdot d=a\cdot BD$. Dividing the both sides by $BD$ gives $\frac cp+\frac dq=a$, i.e. $$cq+dp=apq\tag3$$

Next, let us consider $\triangle{ABC}$. Let $F$ be a point on $AC$ such that $BF\perp AC$. Considering the area of $\triangle{ABE},\triangle{BCE}$ in two ways, we have $$\frac 12\times AE\times BF=\frac 12\times BA\times BE\sin\angle{ABE}$$ $$\frac 12\times CE\times BF=\frac 12\times BC\times BE\sin\angle{CBE}$$ Since $\sin\angle{ABE}=\sin\angle{ACD}=\frac{d}{2R}$ and $\sin\angle{CBE}=\sin\angle{CAD}=\frac{c}{2R}$ where $R$ is the radius of the circle, we can have $$\begin{align}&AE:CE\\\\&=\frac{BA\times BE\sin\angle{ABE}}{BF}:\frac{BC\times BE\sin\angle{CBE}}{BF} \\\\&=\frac{BD}{p}\times\frac{d}{2R}:\frac{BD}{q}\times\frac{c}{2R} \\\\&=dq:cp\end{align}$$

So, we can write $\vec{BE}=\frac{dq\vec{BC}+cp\vec{BA}}{dq+cp}$.

Similarly, considering $\triangle{ADE}$ and $\triangle{ABE}$, we have $$\begin{align}&DE:BE \\\\&=AD\sin\angle{DAC}:AB\sin\angle{BAC} \\\\&=d\times\frac{c}{2R}:\frac{BD}{p}\times\frac{\frac{BD}{q}}{2R} \\\\&=cdpq:BD^2\end{align}$$

Applying the law of cosines to $\triangle{ABC}$, we get $$BA^2+BC^2-2\times BA\times BC\cos(180^\circ-\angle{ADC})=AC^2$$ i.e. $$\frac{BD^2}{p^2}+\frac{BD^2}{q^2}-2\times\frac{BD^2}{pq}\bigg(-\frac{c^2+d^2-a^2}{2cd}\bigg)=a^2$$ i.e. $$BD^2=\frac{a^2}{\frac{1}{p^2}+\frac{1}{q^2}+\frac{c^2+d^2-a^2}{pqcd}}=\frac{a^2cdp^2q^2}{cd(p^2+q^2)+pq(c^2+d^2-a^2)}$$

So, we have $$\frac{BD}{BE}=1+\frac{cdpq}{BD^2}=1+\frac{cdpq}{\frac{a^2cdp^2q^2}{cd(p^2+q^2)+pq(c^2+d^2-a^2)}}=\frac{(cp+dq)(cq+dp)}{a^2pq}=\frac{(cp+dq)apq}{a^2pq}=\frac{cp+dq}{a}$$

So, we can write $\vec{BD}=\frac{cp+dq}{a}\vec{BE}=\frac{cp+dq}{a}\cdot\frac{dq\vec{BC}+cp\vec{BA}}{dq+cp}=\frac{dq}{a}\vec{BC}+\frac{cp}{a}\vec{BA}$, i.e. $$-\vec{DB}=\frac{dq}{a}\bigg(\vec{DC}-\vec{DB}\bigg)+\frac{cp}{a}\bigg(\vec{DA}-\vec{DB}\bigg)$$ i.e. $$(cp+dq-a)\vec{DB}=cp\vec{DA}+dq\vec{DC}$$

Using $(1)(2)$, $$(cp+dq-a)\vec{DB}=cp\bigg(\frac 1p\vec{DX}-\frac{1-p}{p}\vec{DB}\bigg)+dq\bigg(\frac 1q\vec{DY}-\frac{1-q}{q}\vec{DB}\bigg)$$ i.e. $$\vec{DB}=\frac{d\vec{DY}+c\vec{DX}}{-a+c+d}$$

So, from $(1)(2)$, we have $$\vec{DA}=\frac 1p\vec{DX}-\frac{1-p}{p}\cdot \frac{d\vec{DY}+c\vec{DX}}{-a+c+d}=\frac{(-a+d+pc)\vec{DX}-d(1-p)\vec{DY}}{p(-a+c+d)}$$ and $$\vec{DC}=\frac 1q\vec{DY}-\frac{1-q}{q}\cdot \frac{d\vec{DY}+c\vec{DX}}{-a+c+d}=\frac{-c(1-q)\vec{DX}+(-a+c+dq)\vec{DY}}{q(-a+c+d)}$$

So, we finally have $$\vec{DI}=\frac{c}{a+c+d}\vec{DA}+\frac{d}{a+c+d}\vec{DC}$$ $$=\frac{c}{a+c+d}\cdot \frac{(-a+d+pc)\vec{DX}-d(1-p)\vec{DY}}{p(-a+c+d)}+\frac{d}{a+c+d}\cdot \frac{-c(1-q)\vec{DX}+(-a+c+dq)\vec{DY}}{q(-a+c+d)}$$ $$=\underbrace{\frac{c (-a q + c p q + d p q - d p + d q)}{pq(a+c+d)(-a+c+d)}}_{K}\vec{DX}+\underbrace{\frac{d (-a p + c p q + c p - c q + d p q)}{pq(a+c+d)(-a+c+d)}}_{L}\vec{DY}$$ where $$K+L=\frac{p q (c + d)^2 - a (c q + d p)}{pq(a+c+d)(-a+c+d)}=\frac{p q (c + d)^2 - a^2pq}{pq(a+c+d)(-a+c+d)}=1$$

This means that $I$ is on the line $XY$.

Therefore, since $Z=I$, we can finally say that $$\vec{DZ}=\frac{c\vec{DA}+d\vec{DC}}{a+c+d}$$

Answer 2

Notations are in mathematics a matter of choice. They should help and should be chosen so that they fit to the usual human way of always putting letters on the central objects, and be as close as possible to existing formulas that we have applied or will apply hundred times. If a problem starts with "Let $\Delta\; \Theta\epsilon \mathcal G$ be a triangle with centroid $I$..." then everybody will quit that book, and in an exam will use better letters for the vertices and the centroid. I would use a triangle $\Delta ABC$ and denote the centroid by $G$ as everybody does.

---

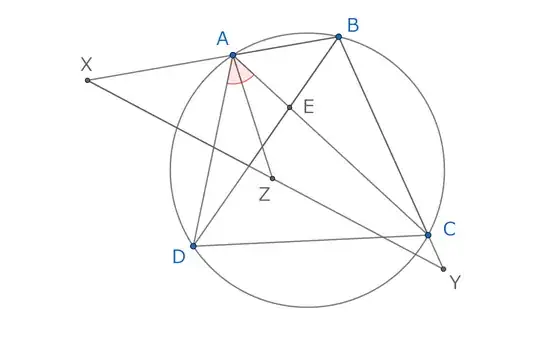
A similar situation is in the present question. Somebody wants to hide a simple property behind a scrambled notation that does not suggest how simple the story may be. My first reaction was of course to use the letters i need at the places i need. Here is a translation into human of the given story:

---

Let $\Delta ABC$ with sides denoted as usual by $a,b,c$ (the lower case letter side corresponds to the side opposite to the vertex denoted by the same upper case letter). Let $I$ be the incenter of $\Delta ABC$.

On the circumcircle of the triangle let $S$ be a point on the arc $\overset{\Large\frown}{BC}$ (not containing $A$). The circle centered in $S$ with radius $SA$ intersects the rays $SB,SC$ in the points $X,Y$ respectively.

Then the points $X,Y,I$ are collinear.

---

---

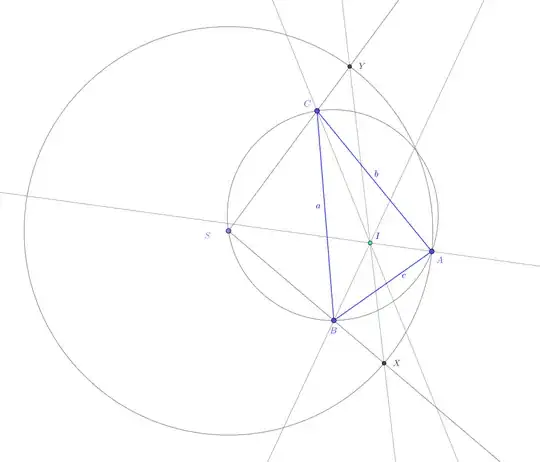
Note: The claimed relations follows now from the known formula for the barycentric coordinates of the incenter (computed w.r.t. $\Delta ABC$ in terms of its side lenghts $a,b,c$): $$ I=[a:b:c]=\frac 1{a+b+c}(a,b,c)\ , $$ where the first notation $[a:b:c]$ uses unnormed barycentric coordinates, the second one being the normed version in vectorial notation. Then we have formally (e.g. by identifying points with their position in the cartesian plane, i.e. using their affixes): $$ I = \frac 1{a+b+c}(aA+bB+cC)\ . $$ Equivalently, for one or for each point $X$ in the plane we have vectorially: $$ \overrightarrow{XI} = \frac 1{a+b+c}\left( a\overrightarrow{XA} + b\overrightarrow{XB} + c\overrightarrow{XC}\right)\ . $$ (Apply this for $X=A$, while at least a posteriori we have $Z=I$, where $Z$ is defined as in the question as $CI\cap XY$.)

---

I will give a proof that is maybe best suited in the context, we use barycentric coordinates. For a short overview:

Barycentric Coordinates for the Impatient, Max Schindler and Evan Chen

Let $S=(s,t,u)$ be the barycentric coordinates of $S$. Since $S\in \overset{\Large\frown}{BC}$, the points $A,S$ are in opposite half-planes w.r.t. the line $BC$. This shows that the signs of $s,t,u$ are $-++$, we will need this below.

A general point will have coordinates $(x,y,z)$. The equation of the circumcircle is (Corollary 9) $0=a^2yz+b^2zx+c^2xy$. So $(s,t,u)$ satisfies this equation, i.e. $$ 0=a^2tu+b^2us+c^2st\ . $$ We list and compute now some points and some lengths of segments: $$ \begin{aligned} A &= (1,0,0)\ ,\\ B &= (0,1,0)\ ,\\ C &= (0,0,1)\ ,\\ I &= [a:b:c]\ ,\\ S &= (s,t,u)\text{ with }1=s+t+u\ ,\ 0=a^2tu+b^2us+c^2st\ ,\\ \overrightarrow {AS} &=(s-1,t-0,u-0)=(s-1,t,u)\ ,\\ SA^2 &=-a^2tu-b^2u(s-1)-c^2(s-1)t=b^2u+c^2t\ ,\\[2mm] s^2\; SA^2 &=s(b^2us+c^2st)=-a^2\; stu\\ &=a^2\Pi^2\qquad\qquad\text{ with }\Pi^2:=-stu\ ,\ \Pi>0\ ,\\ t^2\; SB^2 &=b^2\Pi^2\ ,\\ u^2\; SC^2 &=c^2\Pi^2\ ,\\[3mm] SA &=-\frac as\Pi\ ,\qquad (s<0)\\ SB &=+\frac bt\Pi\ ,\qquad (t>0)\\ SC &=+\frac cu\Pi\ ,\qquad (u>0)\\[3mm] X &=S+\frac {SA}{SB}(B-S)=(s,t,u)-\frac {at}{bs}(-s,1-t,-u) \\ &=\frac 1{bs}\Big(\ s(at+bs)\ ,\ t(at+bs)-at\ ,\ u(at+bs)\ \Big) \\ &=\Big[\ s(at+bs)\ :\ t(at+bs)-at\ :\ u(at+bs)\ \Big]\ ,\\[2mm] Y &=S+\frac {SA}{SC}(C-S)=(s,t,u)-\frac {au}{cs}(-s,-t,1-u) \\ &=\frac 1{cs}\Big(\ s(au+cs)\ ,\ t(au+cs)\ ,\ u(au+cs)-au\ \Big) \\ &=\Big[\ s(au+cs)\ :\ t(au+cs)\ :\ u(au+cs)-au\ \Big]\ . \end{aligned} $$ The needed collinearity is equivalent to the vanishing of the determinant obtained by using (possibly unnormed) coordinates for the points $I,X,Y$. When computing this determinant we omit possible non-zero factors, in this case instead of equality we write $\sim$ to have a short notation, and also not collect factors that in the end do not matter. $$ \begin{aligned} &\begin{vmatrix} a & b & c\\ s(at+bs) & t(at+bs)-at & u(at+bs)\\ s(au+cs) & t(au+cs) & u(au+cs)-au \end{vmatrix} \sim \begin{vmatrix} \frac as\color{gray}{stu} & \frac bt\color{gray}{stu} & \frac cu\color{gray}{stu}\\ 1 & 1-\frac{a}{at+bs} & 1\\ 1 & 1 & 1-\frac {a}{au+cs}\\ \end{vmatrix} \\ &\qquad\sim \begin{vmatrix} atu & bsu-atu & cst-atu\\ 1 & -\frac{a}{at+bs} & 0\\ 1 & 0 & -\frac {a}{au+cs}\\ \end{vmatrix}\sim \begin{vmatrix} atu & bsu-atu & cst-atu\\ at+bs & -a & 0\\ au+cs & 0 & -a\\ \end{vmatrix} \\ &\qquad \sim a^3tu +au(bs-at)(bs+at)+at(cs-au)(cs+au) \\ &\qquad \sim a^2tu +u(b^2s^2-a^2t^2) +t(c^2s^2-a^2u^2) \\ &\qquad = a^2\; tu(1-t-u) + b^2\; s^2u+ c^2\;s^2t \\ &\qquad = s(a^2\; tu + b^2\; us+ c^2\;st)=0\ . \end{aligned} $$ The points $X,Y,I$ are thus collinear.

$\square$

Answer 3

While not a proof, the property of interest here can be demonstrated in Geogebra and thus may clarify the situation to others. The demonstration can be found here, yielding the following image:

The point $D$ is freely movable and sets the radius of the circle 'circ1' (center not shown). The points $B,C,D$ can be moved along this circle, yielding $ABCD$ as a cyclic ("inscribed") quadrilateral. The circle 'circ2' (centered at $B$, passing through $D$) implements the constraint $BX=BY=BD$. The vector $\frac{c\cdot \overrightarrow{DA}+d\cdot \overrightarrow{DC}}{a+c+d}$ is then computed by Geogebra and added to $D$ to obtain point $Z$. (The parallelogram with $D$ at one corner is included to make the vector addition evident.) This point $Z$ is then seen to land at the intersection of the $\angle DAC$'s bisector and the segment $XY$, in agreement with the original vector equation.

If we want to dispense with vectors, we can instead use Geogebra to demonstrate that $Z$ is the incenter of $\triangle ADC$. The demo can be found here, yielding the image below:

Here I've zoomed in and dispensed with some of the labels to make the diagram easier to read. Now the claim to be proven can be stated as such: the incenter of $\triangle ADC$ (that is, the intersection of its three angle bisectors) lies on the segment $XY$. (I've only shown two of these bisectors, again to make for easier visualization.)