3

I am trying to find out if it is possible for there to be a vertex transitive graph, with more than 2 nodes, such that any non-trivial automorphism of it moves all of its nodes? (i.e no node is ever fixed in any non-identity automorphism of the graph)

Also, the graph should be undirected.

The examples which I could construct always have some "swap" or "reflection" symmetry which keeps some node fixed. I wonder if in principle, this is always the case. Alternatively, is there some vertex transitive graph out there such that all points are forced to move in any non-identity automorphism?

RobPratt
  • 50,938
Lisa
  • 129
  • 1
    You are effectively asking if there are nontrivial groups $G$ such that some Cayley graph $X$ of $G$ has $G=Aut(X)$. Such groups indeed exist. For instance, $A_5$ (see an answer here). While your question is natural, you should edit following these guidelines, otherwise, it's likely to be closed. – Moishe Kohan Feb 18 '25 at 13:26
  • But what is the graph? I am interested in what the graph looks like. Are you saying that the Cayley graph corresponding to $A_5$ is such that none of its nodes are fixed in any non-identity automorphism of it? (and thanks for the general advice) – Lisa Feb 18 '25 at 13:35
  • That's right. As for an explicit description of this graph, it's in one of the papers listed by Chris Godsil in his answer. – Moishe Kohan Feb 18 '25 at 13:36
  • I see that Cayley graphs are usually directed graphs (https://mathworld.wolfram.com/CayleyGraph.html). I am looking for an undirected graph example. – Lisa Feb 18 '25 at 13:53
  • Look again in the papers: here the graph is undirected. – Moishe Kohan Feb 18 '25 at 14:34
  • Ok thanks! I will check it. – Lisa Feb 18 '25 at 15:00
  • These are called "graphical regular representations". There are lots of them, that keyword should help you find more information. If you have a more precise question, ask it. – verret Feb 18 '25 at 19:32
  • Ok thanks for the help! – Lisa Feb 19 '25 at 07:59

1 Answers1

5

If I'm not mistaken, this graph of order 12 should do

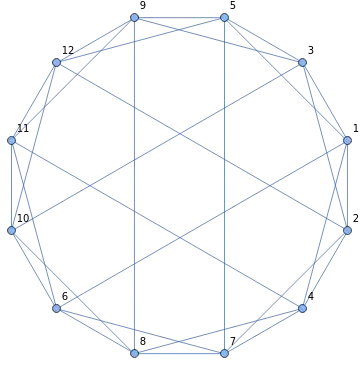
enter image description here

g = Graph[GraphData[{"VertexTransitive",{12,30}} ], VertexLabels->Automatic]

The graph automorphism group has order 12 and is given by

{Cycles[{}],Cycles[{{1,2},{3,4},{5,7},{6,12},{8,9},{10,11}}],Cycles[{{1,3},{2,5},{4,9},{6,10},{7,12},{8,11}}],Cycles[{{1,4,8,10,12,5},{2,7,6,11,9,3}}],Cycles[{{1,5,12,10,8,4},{2,3,9,11,6,7}}],Cycles[{{1,6},{2,8},{3,10},{4,7},{5,11},{9,12}}],Cycles[{{1,7},{2,4},{3,8},{5,6},{9,10},{11,12}}],Cycles[{{1,8,12},{2,6,9},{3,7,11},{4,10,5}}],Cycles[{{1,9},{2,12},{3,5},{4,11},{6,8},{7,10}}],Cycles[{{1,10},{2,11},{3,6},{4,12},{5,8},{7,9}}],Cycles[{{1,11},{2,10},{3,12},{4,6},{5,9},{7,8}}],Cycles[{{1,12,8},{2,9,6},{3,11,7},{4,5,10}}]}

The group is isomorphic to the dihedral group of order 12, i.e. the group of symmetries of a regular hexagon - see https://groupprops.subwiki.org/wiki/Dihedral_group:D12.

The usual presentation is $\langle a,x\mid a^{6}=x^{2}=e,xax=a^{-1}\rangle$, here

x=Cycles[{{1,2},{3,4},{5,7},{6,12},{8,9},{10,11}}]
y=Cycles[{{1,3},{2,5},{4,9},{6,10},{7,12},{8,11}}]
(a=PermutationProduct[x,y])==Cycles[{{1,5,12,10,8,4},{2,3,9,11,6,7}}]
PermutationProduct[x,a,x]==PermutationProduct [a,a,a,a,a]
Michael T
  • 1,742
  • Thanks, misread the definition and now corrected the graph - this one should do. – Michael T Feb 28 '25 at 17:16
  • 3
    BTW: I don't think the question should be closed - questions with 'sufficiently simple' counter examples should be allowed when the alternative is a really deep answer requiring to digest hundreds of pages... – Michael T Feb 28 '25 at 17:18
  • thanks for lifting the close! – Michael T Feb 28 '25 at 17:26
  • Thanks to https://mathematica.stackexchange.com/questions/69829/test-for-group-isomorphism-and-construct-automorphism-groups?rq=1 – Michael T Mar 01 '25 at 10:02
  • 1
    Thank you so much!! This is exactly what I was looking for!! – Lisa Mar 01 '25 at 16:19