6

Consider the closed unit ball in $\mathbb{R}^n$:

$$B_n: = \left\{ x \in \mathbb{R}^n \mid \|x\|_2 \le 1 \right\}.$$

Also define:

$$S_{n,m}(a_1,\dots,a_m,b_1,\dots,b_m) := \left\{x\in\mathbb{R}^n \mid \forall i\in\{1,\dots,m\},a_i\|x\|_1+b_i\|x\|_\infty\le 1 \right\}.$$

I want to choose $m, a_1,\dots,a_m,b_1,\dots,b_m\ge 0$ to minimize the volume of the set $S_{n,m}(a_1,\dots,a_m,b_1,\dots,b_m) \setminus B_n$ subject to $B_n\subseteq S_{n,m}(a_1,\dots,a_m,b_1,\dots,b_m)$.

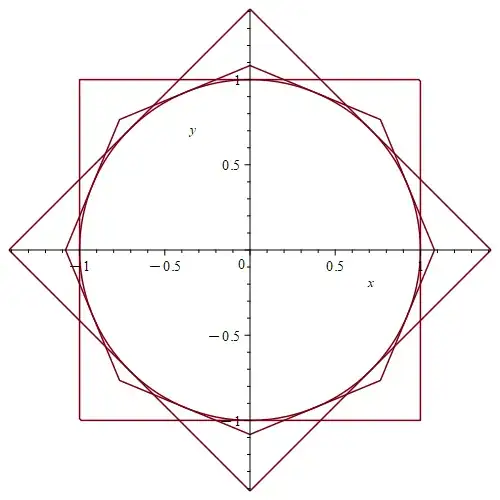
I presume the list should start with $a_1=0,b_1=1$ and $a_2=\frac{1}{\sqrt{n}},b_2=0$ (see e.g. Equivalence of norms in $\mathbb{R^n}$), but how many more items should be in the parameter list? Certainly at least one, as shown by the following plot for $n=2$: n=2 plot

Generated with the following MAPLE code:

plots[implicitplot]([abs(x)+abs(y)+sqrt(2)*max(abs(x),abs(y))=2*(1 + sqrt(2))/sqrt(2 + sqrt(2)),max(abs(x),abs(y))=1 , abs(x)+abs(y)=sqrt(2),x^2+y^2=1],x=-sqrt(2)..sqrt(2),y=-sqrt(2)..sqrt(2));

Here,

$$a_3=\frac{\sqrt{2 + \sqrt{2}}}{2 + 2\sqrt{2}}, \qquad b_3=\sqrt{2}\frac{\sqrt{2 + \sqrt{2}}}{2 + 2\sqrt{2}}$$

I produced these numbers by first noting that the set

$$\left\{ x \in \mathbb{R}^2 \mid \|x\|_1+\sqrt{2}\|x\|_\infty= 1+\sqrt{2} \right\}$$

touched the unit circle in eight places from the inside, then scaling this shape up so that it was bigger than the unit circle. Is this optimal in two dimensions? Does it generalize?

Update: Having thought some more, I now see that $m=\infty$ is optimal. For any $b\le 1$, you can choose $a$ to ensure tangency to the circle. The tangency point is continuous in $b$, and so it traces out the entire circle as $b\rightarrow 0$.

Is there anything special about $m=3$? It certainly seems natural, given that the vertexes are on the same rays for any parameters.

cfp
  • 757
  • First, fix the integer $m$, then worry about optimality. Is that what you are doing? – Rodrigo de Azevedo Feb 08 '25 at 12:53
  • You might want to take a look at Set-theoretic methods in Control – Rodrigo de Azevedo Feb 08 '25 at 12:54
  • 1
    I'm interested in the optimal m too, if it's finite. I expect it's either always 3 or infinity. 3 is natural as any linear combination has vertices on the same rays. Infinity is natural if by taking different weights you can cut more corners. – cfp Feb 08 '25 at 17:11
  • Can you suggest a particular chapter of that book that addresses similar problems? – cfp Feb 08 '25 at 17:14
  • 1
    The chapters on invariant sets and set-theoretic estimation might be interesting. – Rodrigo de Azevedo Feb 08 '25 at 17:20
  • You might find this interesting, too. – Rodrigo de Azevedo Feb 08 '25 at 17:22
  • 1
    It might be useful to think of the convex combination of the two norms and a "radius", say, $$\gamma |x|1 + (1-\gamma) |x|\infty \le r$$ where $\gamma \in [0,1]$ and $r$ is the "radius". Note that $\gamma = \frac{a}{a+b}$. Minimizing the volume could perhaps be thought of as minimizing the "radius" $r$ – Rodrigo de Azevedo Feb 08 '25 at 17:57
  • Having thought some more m=infinity is clearly optimal. The tangency point is continuous in the weights, so you can trace out a circle with infinite combinations. – cfp Feb 08 '25 at 22:31
  • In set-theoretic methods in control theory, one might be interested in finding, say, an ellipsoid that is invariant. In ${\Bbb R}^n$, an ellipsoid would require $\binom{n+1}{2} + n$ parameters to define. If you are interested in polyhedra, there is no inherent bound on their descriptive complexity. You can try polyhedra with $2^{1000}$ faces if you want. Thus, since we don't have infinitely powerful computers, one must impose an upper bound on the descriptive complexity of the polyhedra. In short, fix $m$. – Rodrigo de Azevedo Feb 08 '25 at 22:48

0 Answers0