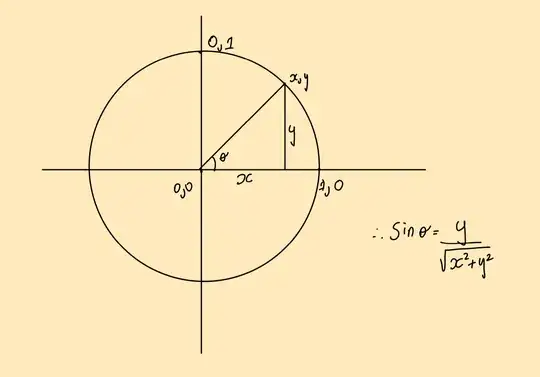
We know that $\sin(120^\circ)=\frac{\sqrt{3}}{2}$. But, Why is this true? Let $ABC$ be a triangle, and say $\angle{ACB}=120^\circ=\theta$
In a right triangle, we can't a construct an angle which is greater than $90^\circ$. Then, how does $\sin(120^\circ)$ or $\sin(150^\circ)$ exist? Also, I am a middle school student.