5

I was reading a textbook on complex dynamics that, in an introductory chapter, demonstrated the complex mapping: $f(z) = \cos(z).$

The text noted that the iteration $ f^{\circ n}(x) $ (infinite composition of $ f $) converges for every real $ x $ to the Dottie number (in fact, on some neighborhood of the real axis in the complex plane).

I was trying to visualize this function, and it appears that there exists a positive real number $ r $ such that $\lim_{n \to \infty} f^{\circ n}(z)$ converges for all $ z $ within the open disk $ \{ z \in \mathbb{C} : |z| \leq r \} $.

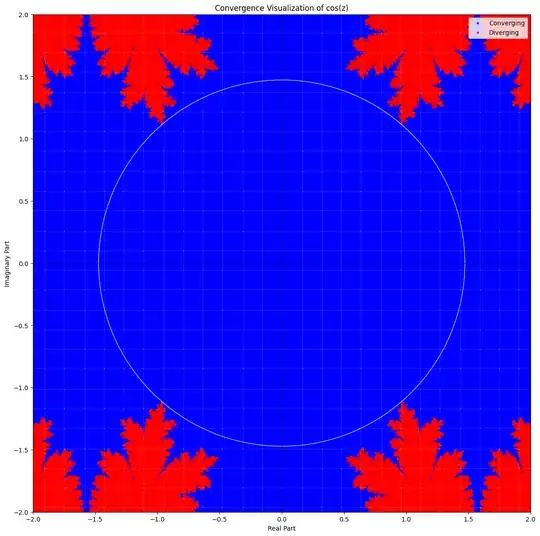
Visualization shows upper bound for $r \approx 1.472$.

My questions are:

  1. Does such a radius $ r \in \mathbb{R^{+}} $ exist, where $ f^{\circ n}(z) $ converges for every $ z \in \mathbb{C} $ with $ |z| < r $?
  2. If so, what is the maximum possible value of this radius?

I tried to analyze the function by converting to polar coordinates, differentiating, and performing a series expansion. However, I struggled with handling such functions properly and failed to derive the right answer.

Any insights into how to determine (or at least approximate) the maximum radius of convergence $ r $ would be greatly appreciated.

user1557030
  • 51
  • 2
    The basin of attraction of the fixed point of the cosine is open and contains zero. So there's certainly an open disk about the origin that's contained in that basin. I doubt that there's a closed form expression for the maximal radius and I imagine you just need to estimate it experimentally, as look like you're able to do. – Mark McClure Feb 02 '25 at 16:19
  • @MarkMcClure maybe there is a way to determine the lower bound for $r_{max}$? For example here I found a proof that $tan(z)$ converges on the whole unit disk. But loogs like that lemma can't be applied to $cos(z)$ as long as $cos(0) \neq 0$. – user1557030 Feb 03 '25 at 13:16

0 Answers0