Find the equation of the parabola whose tangents at $(-1,3)$ and $(1,5)$ are $y+x=2$ and $y-3x=2$ respectively.
(I have solved this by letting the parabola as a general 2nd degree equation, and then $T=0$ wrt point of contacts.)
But I tried using properties of conics, and I ended up here (see image), and couldn't proceed further, as letting the focus and then writing the equations of lines and then equating the angles is too messy. Any hints what should I do after this
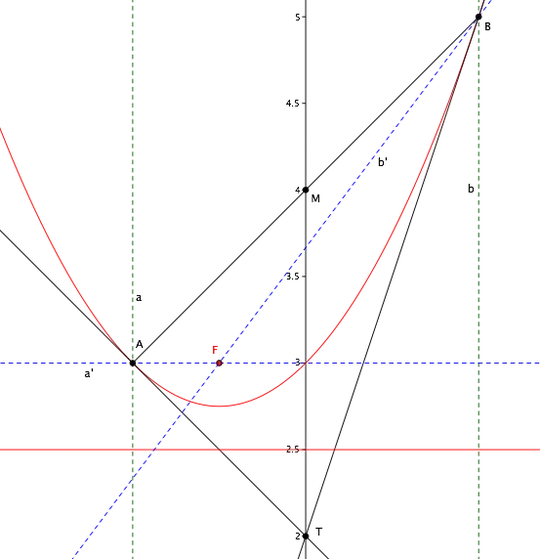
The tangent lines meet at $T=(0,2)$. If $M=(0,4)$ is the midpoint of the given tangency points $A=(-1,3)$ and $B=(1,5)$, line $TM$ is parallel to the axis of the parabola (see here for a proof). Moreover, the midpoint $P=(0,3)$ of $TM$ lies on the parabola.
To find the focus, draw the circle through $A$ and tangent to $BT$ at $T$, then the circle through $B$ and tangent to $AT$ at $T$. The second intersection of those two circles is the focus $F$. This is a consequence of another property of the parabola:
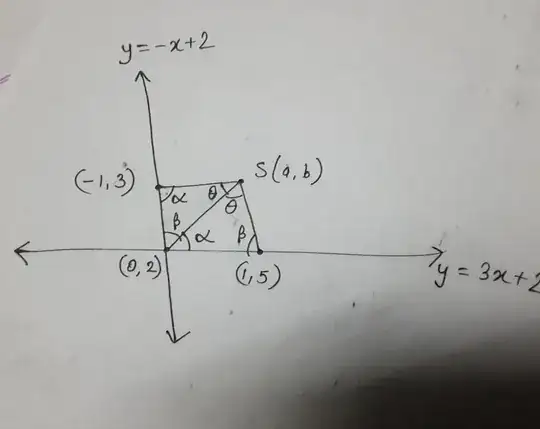
the exterior angle between any two tangents is equal to the angle which either segment of tangent subtends at the focus. (see here for a proof).
In other words: $\angle AFT$ and $\angle BFT$ are both supplementary to $\angle ATB$.
Finally, once focus and axis have been found, it is easy to draw the directrix.
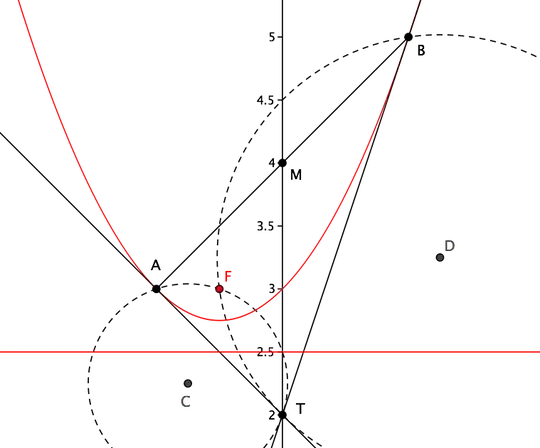
EDIT.
Alternate construction of the focus. Draw two lines $a$ and $b$ through $A$ and $B$ respectively, parallel to $TM$ (and hence parallel to the axis of the parabola). By the reflective property, we know that the reflection $a'$ of $a$ about tangent $AT$, and the reflection $b'$ of $b$ about tangent $BT$, both pass through the focus. We can then construct $a'$, $b'$ and find focus $F$ as their intersection.
Let $A=(-1,3)$ and $C=(1,5)$.
It is easy to compute the intersection point of the tangents, which is point $B=(0,2)$.
If you happen to know (quadratic) Bézier curves, you can obtain at once a parameterization by taking this barycentric representation :
$$M=(1-t)^2 A + 2t(1-t) B + t^2 C$$
$$\pmatrix{x\\y}=(1-t)^2 \pmatrix{-1\\3} + 2t(1-t) \pmatrix{0\\2} + t^2 \pmatrix{1\\5}$$
$$\begin{cases}x&=&2t-1\\y&=&4t^2-4t+3\end{cases}$$
It is easy from there to obtain a cartesian equation of the parabola by "extracting" $t=\frac12(x+1)$ and plugging this expression into the expression of $y$, giving :
$$y=x^2+x+3$$
