3

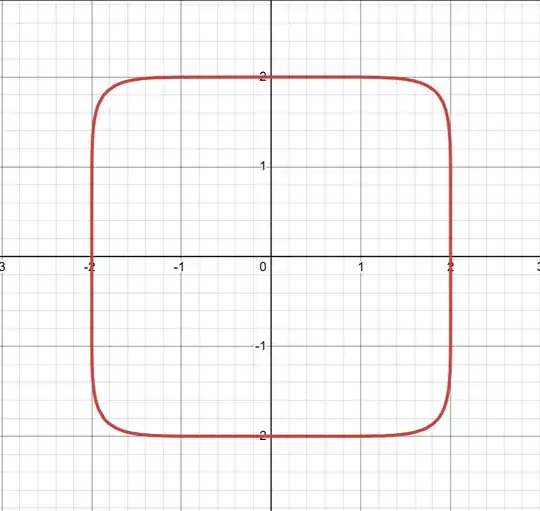
The graph of $x^8 + y^8 = a^8$ looks like this:(if $ a=2$) Graph

From the graph, it seems to me that any tangent to the curve will not intersect the curve. But I want to prove it mathematically, can anyone help?

Update:

I have figured out a probable solution.

Let tangent at $(x_1,y_1)$ meets the curve again at $(x_2, y_2)$

So, the tangents at $(x_1,y_1)$ and at $(x_2,y_2)$ are the same. The tangents are:

$$xx_1^7 + yy^7_1 = a^8$$ $$xx_1^7 + yy^7_1 = a^8$$ As they are the same equation, $$\frac{x_1^7}{x_2^7} = \frac{y_1^7}{y_2^7} = \frac{a^8}{a^8} =1$$

So, $$x_1^7= x_2^7$$ Let, $x_1 = kx_2$, where $k \in \mathbb R$ So, $$k^7x_2^7-x_2^7 = 0$$ $$x_2^7(k^7-1)=0$$ So, we can say $(k^7-1)=0$ and from complex analysis, $1$ has only one real seventh root and that is $1$. So, $x_1$ and $x_2$ are the same point and by contradiction our claim is proved to be true.

Is the proof okay?

M. Saamin Rahman
  • 261
  • 6
    possibly helpful: Prove that no tangent in a convex shape crosses the interior – uhoh Jan 31 '25 at 03:17
  • https://math.stackexchange.com/questions/108393/is-the-composition-of-n-convex-functions-itself-a-convex-function – DanielV Jan 31 '25 at 05:52
  • Just a problem solving tip, the $a$ is just a scaling factor, so you can replace $a^8$ with $1$. – DanielV Jan 31 '25 at 05:55
  • $A$ (with $x(A)^8+y(A)^8=a^8$) has tangent $x(A)^7x+y(A)^7y=a^8$ which also intersects in $$y(A)^6x(A)^6+y(A)^6x(A)^5x+y(A)^5x(A)^6y+y(A)^6x(A)^4x^2+y(A)^5x(A)^5xy+y(A)^4x(A)^6y^2+y(A)^6x(A)^3x^3+y(A)^5x(A)^4x^2y+y(A)^4x(A)^5xy^2+y(A)^3x(A)^6y^3+y(A)^6x(A)^2x^4+y(A)^5x(A)^3x^3y+y(A)^4x(A)^4x^2y^2+y(A)^3x(A)^5xy^3+y(A)^2x(A)^6y^4+y(A)^6x(A)x^5+y(A)^5x(A)^2x^4y+y(A)^4x(A)^3x^3y^2+y(A)^3x(A)^4x^2y^3+y(A)^2x(A)^5xy^4+y(A)x(A)^6y^5+y(A)^6x^6+y(A)^5x(A)x^5y+y(A)^4x(A)^2x^4y^2+y(A)^3x(A)^3x^3y^3+y(A)^2x(A)^4x^2y^4+y(A)x(A)^5xy^5+x(A)^6y^6=0.$$ One strategy could be to show this has no real solutions. – Jan-Magnus Økland Jan 31 '25 at 08:52
  • It does seem to be positive in the positive quadrant, and by symmetry... – Jan-Magnus Økland Jan 31 '25 at 09:23
  • The tangent at $A$ is the linear terms when $A$ is translated to the origin

    $$(x+x(A))^8+(y+y(A))^8-a^8=\x(A)^8+y(A)^8-a^8+8x(A)^7x+8y(A)^8y +\ldots=\8 x(A)^7x+8y(A)^8 +\ldots$$

    or when translated back

    $$(x-x(A)) x(A)^7+(y-y(A)) y(A)^8=\x(A)^7x+y(A)^7y-(x(A)^8+y(A)^8-a^8)-a^8=\x(A)^7x+y(A)^7y-a^8=0.$$

     – Jan-Magnus Økland Feb 02 '25 at 11:15
  • 1
    Why are you assuming the tangent line at $(x_1,y_1)$ is also tangent to the curve at $(x_2,y_2)$? – Gonçalo Feb 02 '25 at 15:28
  • Because the tangent at $(x_1,y_1)$ needs to be the tangent at $(x_2,y_2)$ so that the tangent meets the curve again. @Gonçalo – M. Saamin Rahman Feb 03 '25 at 16:28
  • 1
    It could, in principle, cross the curve at $(x_2,y_2)$. (As an example, consider the tangent to the curve $y=x^3-3x$ at the point $(-1,2)$.) – Gonçalo Feb 03 '25 at 18:23

1 Answers1

1

$$(x-x(A))(y-y(A))(y(A)^6x(A)^6+y(A)^6x(A)^5x+y(A)^5x(A)^6y+y(A)^6x(A)^4x^2+y(A)^5x(A)^5xy+y(A)^4x(A)^6y^2+y(A)^6x(A)^3x^3+y(A)^5x(A)^4x^2y+y(A)^4x(A)^5xy^2+y(A)^3x(A)^6y^3+y(A)^6x(A)^2x^4+y(A)^5x(A)^3x^3y+y(A)^4x(A)^4x^2y^2+y(A)^3x(A)^5xy^3+y(A)^2x(A)^6y^4+y(A)^6x(A)x^5+y(A)^5x(A)^2x^4y+y(A)^4x(A)^3x^3y^2+y(A)^3x(A)^4x^2y^3+y(A)^2x(A)^5xy^4+y(A)x(A)^6y^5+y(A)^6x^6+y(A)^5x(A)x^5y+y(A)^4x(A)^2x^4y^2+y(A)^3x(A)^3x^3y^3+y(A)^2x(A)^4x^2y^4+y(A)x(A)^5xy^5+x(A)^6y^6)$$ is in the ideal $\langle x(A)^8+y(A)^8-1,x^8+y^8-1,x(A)^7x+y(A)^7y-1\rangle,$ signifying that the tangent at $A$ meets the curve in $A=(x(A),y(A))$ doubly and the latter factor vanishes on the other intersections with the curve.

Since this factor is positive in the positive quadrant, and $A$ can't be $(0,0)$ as it's not on the curve, it has no real zeros there. Now, by symmetry this holds in the other quadrants as well.

Jan-Magnus Økland
  • 6,019