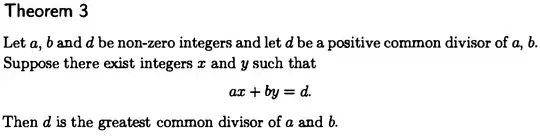I'm trying to understand this theorem:
In other versions of this theorem, it says something like: If $d$ is the GCD of $a,b$, then there exists $x,y\in \Bbb{Z}$ such that $ax+by=d$.
I may be missing something but this theorem seems wrong, for example: Take $2x+4y=4$, there is $x=0,y=1$ but $GCD(2,4)\neq 4$. Is this it or am I missing something? Perhaps the author meant $x,y\in \Bbb{Z}\setminus \{0\}$? I'm not sure if this would change something.