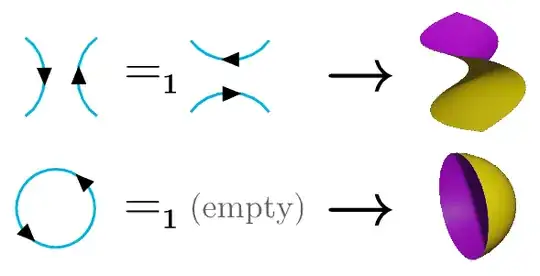String/surface diagrams and the sphere spectrum

Question

I am trying to understand intuitively how the spectrum $\mathbb{S}$ of the stable homotopy groups of spheres arises from the diagrammatic approach hinted at e.g. in John Baez's TWF 102, by explicitly finding the first few stable homotopy groups $\pi_0, \pi_1, \ldots$ Ideally I would want to work out everything up to the third stable homotopy group $\pi_3$ and see where the $24$ comes from, but I'm having trouble already at the second stable homotopy group.^(*)

The idea described in the previous link is to start with the natural numbers, thought of as cardinalities of finite sets, and then categorify, i.e. think of equalities as paths, or motions, transforming a set to itself. These paths are then treated as objects in their own right, one dimension higher. Since there is a notion of when two paths are "close" to each other, the paths have their own equivalences, which then generate new objects one dimension higher, and so on.

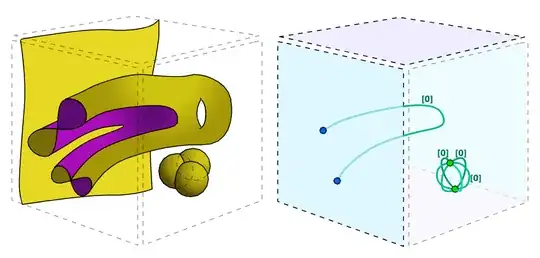
When one does this and adds negative elements to get the integers $\mathbb{Z}$, plus the paths corresponding to the ways of cancelling them, plus the surfaces corresponding to the ways of cancelling the new paths, etc., the resulting structure is equivalent to the sphere spectrum $\mathbb{S}$, with the group structure given by disjoint union (I believe the ring structure can also be defined by some variation of Cartesian product). As Baez mentions, this has led some people to consider $\mathbb{S}$ as the "true integers" in some sense, see e.g. this MathOverflow question. On the other hand, this gives an alternate way to visualize elements of $\pi_n \in \mathbb{S}$ geometrically in terms of $n$-dimensional hypersurfaces in $n+1$ dimensions.

The groups $\pi_0$ and $\pi_1$

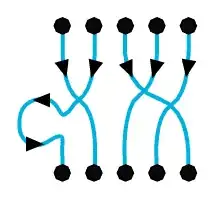
I believe I have a good grasp of how the zeroth and first stable homotopy groups of $\mathbb{S}$ arise. To start with, a natural number $n$ is represented as a set of $n$ points arranged in a straight line. The symmetries of this set consist of all the ways of permuting the points, and the corresponding motions are represented as sets of one-dimensional lines in the plane, connecting each starting point to its final position. To keep track of the direction of motion, the lines are assigned an orientation from top to bottom. This is called a string diagram or line diagram.

Lines are allowed to cross each other ^($\dagger$), with no distinction between over-crossings and under-crossings; roughly speaking two line diagrams are regarded as equivalent (for which I'll use the notation $=_\text{1D}$) if one can smoothly deform the first diagram to the other without creating any cusp singularities in the process, i.e. using the second and third Reidemeister moves to move the crossings around (an intuitive reasoning for not allowing the first Reidemeister move is that at some point during the deformation, a cusp is created where the tangent vector of a single line is not well-defined, thus the diagram can't be properly interpreted as representing a smooth motion of points with constant speed. The appropriate mathematical concept defining a valid string diagram is that of an immersion of oriented intervals into $\mathbb{R}^2$).

This is a complicated structure, since for each number $n$ there are $n!$ different permutations and thus $n!$ possible string diagrams up to deformation, but much of that structure collapses when one adds negative points. A set with $n$ regular (positive) points and $m$ negative points represents the integer $n-m$. Since $n-m = (n+1)-(m+1)$, there are new allowed lines corresponding to creating or cancelling a pair of opossitely-signed points.

In order to be able to assign a consistent orientation to the new creation/annihilation lines, the lines coming out of negative points are forced to have the opposite orientation, as if the points were moving backwards in time; a similar convention is used in particle physics to draw Feynman diagrams containing antiparticles.

Since a state with two opossitely-signed points very close to each other should be considered "similar" to a state with no points at all, the allowed deformations of the paths include two new ones:

These two deformations allow for the isolation of a simple crossing, as follows:

This isolated simple crossing in fact corresponds to the complex Hopf fibration $\eta \in \pi_1$ generating the first stable homotopy group of the sphere spectrum. So all sets of lines from $n$ to $n$ can be deformed in this way into the disjoint union of $n$ straight vertical lines plus a bunch of isolated simple crossings. Two of these isolated simple crossings cancel as follows:

corresponding to the equation $2\eta=0$ in $\mathbb{S}$.

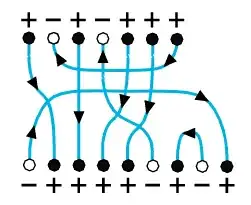
Thus there exists an algorithm that reduces any valid configuration of lines in the plane to a canonical representative in $\pi_0 \oplus \pi_1 \simeq \mathbb{Z} \oplus \mathbb{Z}_2 \eta$:

1. Deform the lines if necessary so that there are only simple crossings.

2. Isolate all crossings as above.

3. Cancel the crossings in pairs until we are left with at most one.

4. Cancel pairs of positive/negative points and their associated lines.

The resulting element is the resulting number $n$ of lines with their associated points (so $n$ can be positive, zero or negative) if there is no isolated crossing at the end of the process, or $n+\eta$ if there is one. The presence or absence of $\eta$ is related to the concept of parity of a permutation.

The group $\pi_2$

The second stable homotopy group would be obtained by "categorifying" again, taking all valid 1D-deformations of the lines and promoting them to the surfaces traced out by these deformations in three-dimensional space, for example:

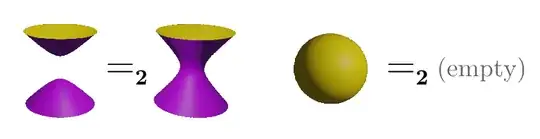
Since the lines are oriented, the surfaces will also be oriented, which I indicate by coloring each side with a different color (yellow/purple as in the famous sphere eversion movie). The allowed 2D-deformations for surfaces (for which I'll use the notation $=_\text{2D}$) include both "spherical" creation/annihilation (John Baez explicitly mentions this one) and "hyperbolic" joining/splitting:

plus the obvious topological motions, disallowing cusps, creases and similar singularities (i.e., the surfaces must remain immersions at every instant of time). So for example a torus, or really any higher genus closed surface without crossings, is 2D-deformation-equivalent to a sphere, which is in turn equivalent to the empty set. This lends credibility to the idea that only a few surfaces survive the reduction process.

The generator $\eta^2$ of the second stable homotopy group of $\mathbb{S}$ is represented by the Cartesian product of two $\eta$s, which is 2D-deformation-equivalent to the surface obtained by taking the Cartesian product of $\eta$ by an interval, twisting one of the ends by $360$ degrees and gluing both ends:

As before, there is a reduction process that takes as input a valid surface diagram and outputs a canonical representative, formed by a disjoint union of planes, the product of $\eta$ times an interval, and the above $\eta^2$ generator. However, so far I've been unable to figure out the steps of the process.

Generically two planes cross in a line, and three planes cross in a point. So in the general case, after slightly deforming the surfaces if necessary, the "crossing locus" is something like a graph, whose internal nodes where three surfaces cross have valence $6$ (and the external nodes have valence $1$), and where closed loops with no nodes are also allowed. Most likely this description would have to be supplemented with some information that accounts for orientation, to distinguish between $\eta^2$ and the trivial $\eta\times$ circle (I guess finding the proper description can be considered as part of my question). The internal nodes really do arise within valid configurations, e.g. there is a single internal node in the surface corresponding to the third Reidemester move (marked in green):

However, none of the objects (planes, $\eta \times \text{interval}$ and $\eta^2$) in the supposed final configuration have any internal nodes, so there must be a way to cancel them using allowed 2D motions.

Question

My question is:

What is the algorithm that reduces any valid two-dimensional surface diagram to a canonical representative in $\mathbb{Z} \oplus \mathbb{Z}_2 \eta \oplus \mathbb{Z}_2 \eta^2 \subset \mathbb{S}$?

In particular, what element do we obtain when applying it to the third-Reidemester-move surface? (it should be either $3+\eta$ or $3+\eta+\eta^2$). For the purposes of answering the question you may take as allowed motions only the ones I described above (regular homotopies between immersions plus the spherical and hyperbolic moves), unless the "obviously correct answer" uses some other motion.

If there is a reference that deals with this stuff, I would love to hear about it, especially if it also treats higher stable homotopy groups such as $\pi_3$.

---

(*): This is probably irrelevant, but the way I arrived at this question is by thinking about what would be the correct higher-dimensional generalization of Penrose diagrams, describing the categorification of (super) vector spaces. Some of them should arise as linear combinations of the diagrams in this question, so I need to understand them first.

($\dagger$): Actually, John Baez describes these line diagrams, or "tangles", as embedded in a space of higher dimension (at least four), so that everything is smooth, the crossings don't really exist and are just an artifact of the projection to 2D. But then everything becomes trivial when one adds negative elements, since the first Reidemester move is now allowed and $\eta$ can be turned into a circle. If one adopts this interpretation, some extra information is needed such as a stable framing (and this is enough since there is a known relationship between cobordisms of stably framed manifolds and the sphere spectrum). EDIT: The alternate interpretation in this question can be justified from the proof of Theorem A in this article by U. Koschorke, where the sphere spectrum is shown to correspond to oriented bordisms of immersed manifolds in codimension $1$. This lets us sidestep the tricky notion of a stable framing, and describe the sphere spectrum in terms of more familiar concepts such as orientations and crossings in a reasonably low dimension. I learned about this thanks to this post by Scott Carter, from the MO thread linked in Qiaochu Yuan's answer.

Answer 1

Not a complete answer, but some pointers to where to look: you are looking at a version of the Pontryagin-Thom isomorphism between the stable homotopy groups of spheres and framed cobordism, specifically the version you get from the cobordism hypothesis. I tried to describe what some of this looks like more concretely on MO here but I'm not sure I succeeded.

Here is an extremely abstract formulation. The sphere spectrum $\mathbb{S}$ is "the free symmetric monoidal $\infty$-groupoid on a point." There is another object called $\text{Bord}$ built out of cobordisms of framed manifolds, which according to the cobordism hypothesis is "the free symmetric monoidal $\infty$-category with all duals on a point." Duals are weakenings of inverses, so these universal properties imply that there is a canonical map

$$\text{Bord} \to \mathbb{S}$$

and this map reproduces the Pontryagin-Thom isomorphism, as well as being the avatar in all dimensions of the map you're looking for that turns a complicated diagram of framed manifolds into some data involving the stable homotopy group of spheres.

From this point of view, as described here on MO, $\pi_3(\mathbb{S})$ is generated by $S^3 \cong SU(2)$ with its Lie group framing, and it has order $24$ because there exists a framed cobordism from $24$ copies of $S^3$ to the empty manifold which can be constructed from a vector field with $24$ isolated zeroes (the Euler characteristic) on a K3 surface. I have no idea how to visualize any of this, personally.

The cobordism hypothesis is highly relevant to your question about categorified Penrose diagrams acting on categorified vector spaces; you are looking for some version of topological quantum field theory.

Answer 2

After taking the time to fully read and digest the Koschorke paper mentioned in my update and some related ones, I think I can finally make an attempt at an answer. I'm not fully satisfied with it but I believe it is at least correct in essence.

The main intuition is that surfaces up to oriented cobordism behave "like soap bubbles", similarly to how surfaces up to homeomorphism behave "like rubbersheets". As already seen in the one-dimensional case, by creating, destroying, merging and splitting the surface using spherical and hyperbolic motions we can reshape the ordinarily embedded part (away from the crossing locus) to pretty much anything we want. This means that almost everything is determined by the behavior in the neighborhood of the crossing locus. These loci turn out to retain some of the bubbliness of their parent surfaces, and can be split and merged at will; however, they can only be created or destroyed if they are untwisted in a certain specific sense, a fact which ultimately leads to the survival of $\eta^2$. The trickiest part for me has been handling the case with boundary, since not all possible surface diagrams one could think of are valid (come from allowed motions).

The group $\pi_2$

A surface diagram, arising from the smooth motion of a string diagram, can be formally described as the immersion of an oriented surface with (possibly empty) boundary and corners into a cube in $\mathbb{R}^3$, such that the boundary (made of string diagrams) lies within four specific faces of the cube forming a ring around it, and the corners (made of positive or negative points) lie within the cube edges delimiting two adjacent such faces. The valid motions or 2D-deformations are as described in my question, and come from oriented bordisms between these surface immersions.

As I mentioned in my question, after a small perturbation, the crossing locus will consist of a graph made of edges and nodes; the edges are made of double points, and the nodes can be $6$-valent or $1$-valent. The $6$-valent nodes correspond to triple points, whereas the $1$-valent nodes can only be in the boundary, and are identified with the simple crossings of the copy of $\pi_1$ living in that boundary. Nodes lying in two adjacent faces of the cube cannot be directly connected by an edge, as this leads to a surface traced by a forbidden motion in a string diagram. This restriction doesn't apply to nodes lying in opposite faces of the cube, as shown by e.g. the surface traced by the identity motion on an isolated crossing.

This graph has further structure: the six edges surrounding a node come from three smooth curve segments intersecting at that node, so there is a relationship that identifies the edges adjacent to any node in pairs. This relationship creates a partition of the set of edges such that the closure of any part forms a smooth curve, that is either closed or having both of its ends on the boundary. In the closed case these have been called "daisy graphs" in this paper by Li, which shows that for an oriented surface each smooth curve (or "transverse component") must necessarily pass through an even number of nodes.

Consider the intersection of the surface with a small tubular neighborhood around one of these curves. The X-shaped cross-section of this intersection will twist a number $n$ of full turns as we go around the curve (half-turns are not permitted since the resulting surface would be nonorientable). To indicate this, we add the label $[n]$ to the curve. We will also indicate each of the four possible components of the boundary on which $1$-valent nodes can lie (the faces of the cube) as a blob surrounding these nodes, which is colored light blue or dark blue so as to distinguish between the two pairs of opposite faces, as in the picture above. We call a graph equipped with this extra information an "extended crossing locus".

The allowed 2D-deformations induce equivalences between extended crossing loci, which I'll denote using the symbol $=_{1\frac12}$ since they are motions of one-dimensional graphs which also retain some underlying 2D information:

Labels that don't matter are omitted. The blue blobs stand for any boundary component (light or dark). The 2D motions generating the equivalences are easy to come up with in most cases, some examples of them are depicted in Theorem 3.1 of this paper by Hass & Hughies. Perhaps the most non-obvious ones are motions F and G, which reduce the twist of a loop by $2$ full turns or $720$ degrees: it comes from the famous Dirac's belt trick, if we think of the neighborhood of the loop as made of two "belts".

The algorithm

The reduction algorithm I came up with is the following one. Consider the extended crossing locus:

1. Use motions C and E to delete as many pairs of $1$-valent nodes as possible, until left with either no $1$-valent nodes or a single pair of $1$-valent nodes located in opposite faces.

2. If there are still $1$-valent nodes, delete as many triple points as possible by motions C and D, using the reverse of E to temporarily create some extra nodes if necessary, and delete the redundant nodes again using C and E.

3. Reduce the twist between the pair of $1$-valent nodes to either $0$ or $1$ using motion G, and if the remaining twist is $1$, extract it in a separate loop using motion C.

Here is an example of the two previous steps for the third-Reidemeister-move surface, which shows that the answer to my subquestion is $3+\eta$ ^($*$). The twists are always zero, so I omit them in the intermediate steps for clarity:

After the first and second steps one is left with at most one curve connecting two opposite boundary components, corresponding to $\eta \times \text{ interval}$, and a separate graph featuring only $6$-valent nodes, corresponding to a closed surface. It is a theorem of Banchoff that the number of triple points for a closed immersed surface is equal to the Euler characteristic of the surface modulo $2$; in our oriented case, there is then an even number of triple points, so we can cancel them two-by-two even if there is no point on the boundary.

4. Cancel all triple points in pairs using motion A, making use of motion C as needed to arrange the curves to look like A's left-hand side.

The remaining extended crossing locus will consist of a bunch of disjoint closed loops.

5. Join all loops into one using motion C.

6. Reduce the twist of the remaining loop to either $0$ or $1$ using motion F. If the twist is $0$, delete the loop using motion B.

Going back to the original surface description, if the twist was $0$, all that remains is an ordinarily embedded surface with boundary and corners. By a straightforward application of the spherical and hyperbolic motions, we can cancel any possible nonzero genus and be left with a bunch of oriented squares, representing the integer $n \in \pi_0$. If the twist is $1$, there is an additional disjoint $\eta^2 \in \pi_2$. There is also the possible $\eta \in \pi_1$ we had set aside before step 4.

Modulo any mistakes, this describes an algorithm that reduces an arbitrary valid surface diagram to a canonical element of $\mathbb{Z} \oplus \eta \mathbb{Z}_2 \oplus \eta^2 \mathbb{Z}_2 \subset \mathbb{S}$.

---

Higher groups $\pi_3, \pi_4, \ldots$

For completeness I'll list here what I have learned about higher groups. In the case of $\pi_3$, the generator $\nu$ turns out to be given by a capped sphere eversion: this is the immersed manifold traced by starting with a point, expanding it into a sphere, everting the sphere following the Froissart-Morin procedure, and shrinking it back to a point (by a funny coincidence I linked to a sphere eversion movie in my question, but I don't know if that sphere eversion also gives a generator of $\pi_3$ or it has to be specifically the Froissart-Morin one). I haven't read it yet, but there is seemingly a whole book (!) by Scott Carter dedicated to describing this eversion. In particular the crossing locus is a two-dimensional nonorientable surface of double points in $\mathbb{R}^4$, featuring a loop of triple points and a single quadruple point.

As Qiaochu Yuan mentions, the equation $24\nu = 0$ can be seen to come from the existence of the $K3$ surface, which is four-dimensional as a real manifold and has Euler characteristic $24$. Some immersion of this manifold punctured $24$ times into $\mathbb{R}^5$ will define a "movie" in $\mathbb{R}^4$, where twenty-four capped sphere eversions combine and are annihilated into nothing. This is at the edge of what I would consider a reasonable visualization but I think it can be done, especially if we consider only the evolution of the crossing locus, as there are methods to represent 4D objects evolving in time using e.g. color-coded data.

One can go even higher, although most stuff ceases to be visualizable:

• The groups $\pi_4, \pi_5$ are both trivial, so all closed manifolds in those dimensions must be equivalent to the empty one by the appropriate reduction algorithm. The order-two generator $\nu^2 \in \pi_6$ would be given by the Cartesian product of two capped sphere eversions. I don't know the oriented manifold that would realize the equation $2\nu^2=0$.

• Note that the real, complex and quaternionic Hopf maps $2, \eta, \nu \in \mathbb{S}$ can be defined as the capped sphere eversions of the spheres $S^{-1} \simeq \text{(empty)}, S^0 \simeq \text{(two points)}$ and $S^2$ respectively (the words "expand" and "shrink" in my description of the eversion must be interpreted a bit more liberally in the case of $S^{-1}$). Since according to Wikipedia the only other sphere that can be everted is $S^6$, my guess is that the remaining octonionic Hopf map $\sigma \in \pi_7$ will also correspond to one such eversion. There exists an "octonionic $K3$ manifold", found in this MathOverflow post, that realizes the equation $240\sigma = 0$ as a cobordism; that octonionic $K3$ with $240$ punctures would define the motions in $\mathbb{R}^8$ that annihilate a total of $240$ capped $6$-sphere eversions. I think trying to visualize this "movie" in any significant way is hopeless since we need eight dimensions.

---

($*$): The reason I was puzzled by this particular surface is because I mistakenly thought that objects lying on the boundary had to be fixed, and didn't realize that they have some limited freedom of movement. This was a stupid mistake in hindsight since I already knew that boundary points can move and even cancel in the one-dimensional case, provided two points of the same sign do not pass through each other. I'm still a little confused on which specific motions are allowed when there is a boundary, and it could be that the third-Reidemester-move surface is not actually a valid surface diagram. But the surface consisting of an $\eta \times \text{interval}$ obliquely intersecting a plane is definitely allowed, and it still has a single triple point, so motion D is a necessary part of the algorithm.