3

About a month ago, I came up with a beautiful parabola property and proved it myself, and then I discovered two days later that it generalizes to all the conic sections, but I still haven't proven it yet.

I think it is possible to prove this by brute force with analytical geometry, but I think an elementary theorem like this deserves a proper geometric proof.

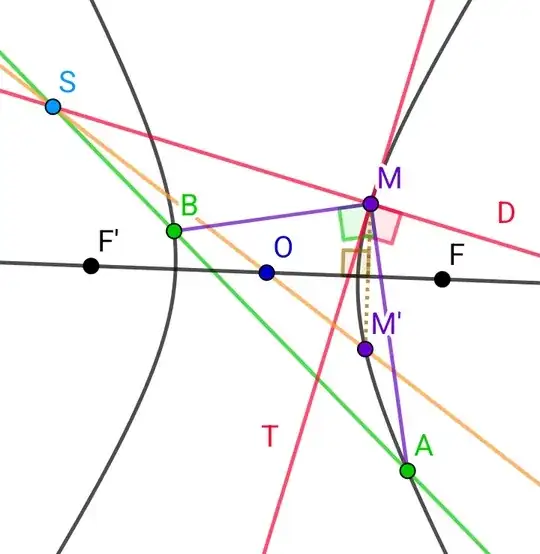
Theorem: If three points are selected on a conic section such that they form the vertices of a right triangle, then the hypotenuse of this triangle passes through a fixed point, regardless of how the two vertices of the acute angles are moved, as long as the vertex of the right angle remains fixed. Moreover, if the vertex of the right angle is moved along the conic section, the locus of the point that was fixed is another conic section that is a homothetic transformation of the original conic, with the center of homothety being the center of the original conic section.

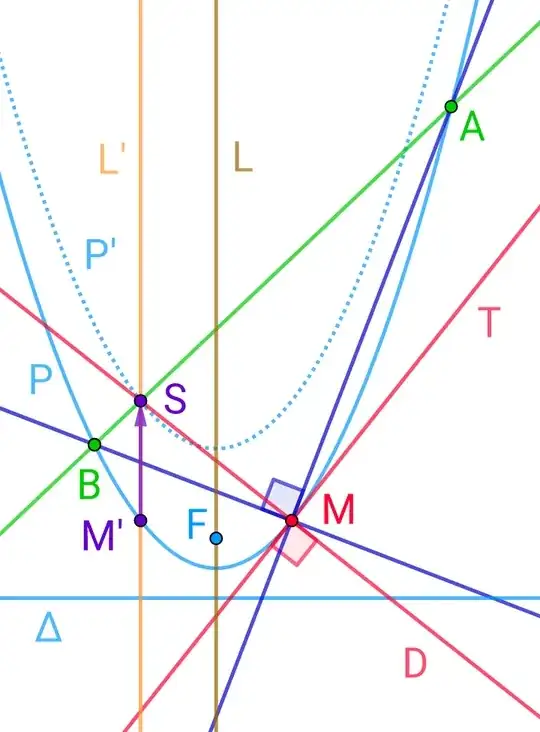
enter image description here enter image description here In the case of a parabola, a similar parabola will arise and the theorem can be formulated like this: Theorem: If three points are selected on a parabola such that they form the vertices of a right triangle, the hypotenuse of this triangle passes through a fixed point regardless of how the two vertices of the acute angles move, as long as the vertex of the right angle remains fixed. Moreover, if the vertex of the right angle moves along the parabola, the locus of the point that was fixed is another parabola, which is a translation of the original parabola along a vector parallel to its axis of symmetry.

Given: Let $P$ be a parabola with focus $F$, directrix $\Delta$, and axis of symmetry $L$. Let $A, M, B$ be three points on $P$, where $M$ is a fixed point on $P$, and $A, B$ move along $P$ such that the points $A, M, B$ always satisfy $\angle AMB = 90^\circ$.

Required:

  1. Prove that the variable line $AB$ passes through a fixed point $S$ during the motion of $A$ and $B$.

  2. Prove that the locus of the point $S$ as $M$ moves along $P$ (while maintaining the condition $\angle AMB = 90^\circ$) is a parabola $P'$ that is a translation of the original parabola $P$ along a vector parallel to the axis of symmetry $L$, with a magnitude equal to twice the distance between $F$ and $\Delta$.

enter image description here

I have proven the case of the parabola using analytic geometry I will put my solution in the answers

My question consists of 3 things:

  1. What is the percentage of similarity in the case of a conic sections that differs from a parabola?

  2. Is there a geometric proof of the theorem?

  3. Is this theorem already known earlier?

زكريا حسناوي
  • 4,060
  • 7
  • 25
  • Theorem (Converse): The converse theorem also true: If three points are selected on a parabola, where one of the points is fixed, and the other two move along the parabola such that these points form the vertices of a triangle with one angle having a constant measure (the angle associated with the fixed point), and the side opposite to that angle passes through a fixed point during the motion, then the mentioned angle with the constant measure must be a right angle. – زكريا حسناوي Jan 27 '25 at 08:48
  • Application: Using construction, we can deduce that the three points forming a right inscribed angle on a conic section cannot all lie on the same side of its primary axis of symmetry. – زكريا حسناوي Jan 27 '25 at 08:51
  • 1
    Based on some quick-and-dirty coordinate bashing in Mathematica, I believe we can say the following (for non-circular conics): Let $F$ be a focus of the conic. Let $C$ be a right-angle vertex on the conic, let $C'$ be the reflection of $C$ in the directrix corresponding to $F$, and let $C''$ be the dilation of $C'$ in $F$, with scale factor $e^2/(e^2-2)$ (where $e$ is the conic's eccentricity). Point $C''$ lies on all the described hypotenuses. ... For now, I'll leave a geometric proof to others. – Blue Jan 27 '25 at 10:02
  • 1
    In fact it is a known result : see the question and the answer by Brainjam here. – Jean Marie Jan 27 '25 at 10:13
  • Now I tested your result on Geogebra and your calculations were correct (just reverse the signal), Mashallah, you are brilliant and you were able to reach this quickly @Blue – زكريا حسناوي Jan 27 '25 at 10:35
  • Thank you @JeanMarie, This answers my question 3 – زكريا حسناوي Jan 27 '25 at 10:35
  • 1
    @JeanMarie: Comments to that question refer back to one from 2016 (about ellipses), which has an answer (by me!) that identifies the fixed pt as the intersection of the normal and a diagonal of the inscribed rectangle determined by the right-angle vertex ($C$ in my above comment). By my earlier observation, the normal and diagonal concur w/the line through the focus and the directrix-reflection of $C$. Thus, we have a (likely already-known) way to construct a normal using a focus & directrix. Nifty! – Blue Jan 27 '25 at 12:58
  • 1
    A more precise answer : The result you have (re)discovered is "Frégier's theorem for conics". – Jean Marie Feb 01 '25 at 13:03

0 Answers0