From the answer https://math.stackexchange.com/a/3743490/ it is possible to embed isometrically (bent but not stretched) Penrose triangle into curved three dimensional space, something called "nil geometry".
I wonder if the impossible cube also can be embedded isometrically into a curved three-dimensional space.
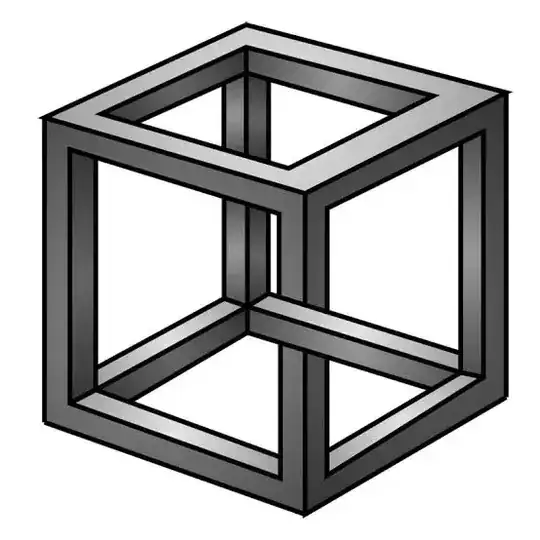
▲ An impossible cube, with adjacent squares having linking number $1$ or $-1$.