An integral related to a seashell: $\int_0^\pi\ln(x-\sin x)dx$

Question

I am looking for a closed form for

$$I=\int_0^\pi\ln(x-\sin x)dx=-4.78467028887\dots$$

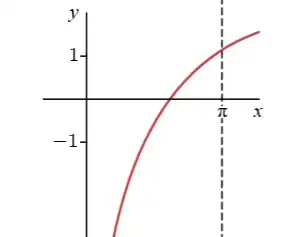
Here is a graph of the integrand:

Context, and why I suspect $I$ has a closed form

On a circle, choose $n$ evenly spaced points, with one point at the bottom of the circle. Through each point and the bottom point, draw a circular arc tangent to the circle's vertical diameter. Here is an example with $n=12$.

Numerical investigation suggests that if the average area of the regions is $\frac14e^{-I/\pi}=1.14649917333\dots$ (that is, the area of the circle is $\frac{n}{4}e^{-I/\pi}$), then as $n\to\infty$, the product of the areas of the regions converges to $2$. (If the average area is less than this, then the product converges to $0$; if the average area is greater than this, then the product diverges.)

I suspect that $I$ has a closed form, because in my previous explorations of products of areas in circles, I have found various exotic closed forms: example 1, example 2, example 3, example 4.

My attempt

A search on Approach Zero turned up nothing similar. Wolfram Alpha does not evaluate the definite nor indefinite integral. Other than that, I don't know what to do.

---

Note: Some of the comments refer to the original version of this question, which asked for a closed form for $\int_{-\pi/2}^{\pi/2}\ln\left(x(\cot x)\csc^2x-\cot^2x\right)dx$. The comments indicated that this integral can be simplified to $\int_0^\pi\ln(x-\sin x)dx+\pi\ln 2$.

Answer 1

This is not an answer.

Itis interesting to look at the series expansion $$\log (x-\sin (x))=\log \left(\frac{x^3}{6}\right)-\frac{x^2}{20}-\frac{x^4}{16800}+\frac{x^6}{756000}+\frac{89x^8}{3104640000}+O\left(x^{10}\right)$$ which gives tight bounds.

Integrating $$\int_0^\pi \log (x-\sin (x))\,dx=-\pi \log \left(\frac{6 e^3}{\pi^3}\right)-\frac{\pi ^3}{60}-\frac{\pi ^5}{84000}+\frac{\pi ^7}{5292000}+\frac{89 \pi ^9}{27941760000}$$ which is $-4.784680041$.

Using the expansion to $O\left(x^{100}\right)$ gives $\color{red}{-4.784670288876693048728862265}50$

Alas, I did not find what are the coefficients of the series expansion.

Answer 2

Via the Laplace transform and integration by parts, one finds: $$I=\pi\ln(\pi)-\int_0^\pi x\frac{1-\cos(x)}{1-\sin(x)}dx=\int_0^\pi\int_0^\infty x(1-\cos(x))e^{t(\sin(x)-x)}dtdx=\int_0^\infty-\frac\pi te^{-\pi t}+\frac1t\int_0^\pi e^{t(\sin(x)-x)}dxdt$$ The double integral converges and the inside integral uses the Anger $J_v(z)$/Weber $E_v(z)$ functions. Therefore: $$\int_0^\pi\ln(x-\sin(x))dx=\pi\int_0^\infty\frac{J_{it}(it)+iE_{it}(it)-e^{-\pi t}}tdt$$

---

One can integrate the inverse of the integrand as $f(e^x)$ where $f(x)-\sin(f(x))=x$. The integral is split into where the $\ln(x-\sin(x))$ is positive/negative: $$I=\int_0^\frac\pi2\ln(x-\sin(x))dx= \int_0^a\ln(x-\sin(x))dx+\int_a^\pi\ln(x-\sin(x))dx+\pi\ln(2)=\pi\ln(2)-\int_{-\infty}^0f(e^x)dx+\pi\ln(\pi)-\int_0^{\ln(\pi)}f(e^x)dx$$ $y=f(x)$ has a Fourier series: $$y-\sin(y)\implies y=x+\sum_{n=1}^\infty\frac2nJ_n(n)\sin(nx)$$ and one finds the following using the sine integral function and Bessel function of the first kind. Here $\ln(a-\sin(a))=0$: $$\int_a^\pi\ln(x-\sin(x)dx= \pi\ln(\pi)-\pi+1-\sum_{n=1}^\infty \frac2n J_n(n) (\operatorname{Si}(π n)-\operatorname{Si}(n))$$ as shown here: $$\int_0^a\ln(x-\sin(x))dx= 1+\sum_{n=1}^\infty \frac2n J_n(n)\operatorname {Si}(n)$$ seems to converge slowly, but the Fourier series converges globally, so the series should be valid. Therefore, it would be that: $$\int_0^\pi\ln(x-\sin(x))dx= \pi\ln(\pi)- \pi -\sum_{n=1}^\infty \frac2n J_n(n)\operatorname {Si}(\pi n)$$

---

Another method is expanding $\ln(1-y)$, switching the integral/sum as numerically shown here, and evaluating $\int_0^\pi(\frac{\sin(x)}x)^ndx$ via:

$\displaystyle\int\limits_0^\pi\left(\frac{\sin x}{x}\right)^n dx = \frac{1}{(n-1)!}\sum\limits_{k=0}^{\lfloor (n-1)/2\rfloor}(-1)^k{\binom n k}\left(\frac{n}{2}-k\right)^{n-1}\text{Si}((n-2k)\pi)$

$$I=\pi\ln(\pi)-\pi+\int_0^\pi\ln\left(1-\frac{\sin(x)}x\right)dx=\pi\ln(\pi)-\pi-\sum_{n=1}^\infty\frac1n\int_0^\pi\left(\frac{\sin(x)}x\right)^ndx= \pi\ln(\pi)-\pi-\sum_{n=1}^\infty\sum_{k=0}^{\left\lfloor\frac{n-1}2\right\rfloor}\frac{(-1)^k}{k! (n-k)!}\left(\frac n2-k\right)^{n-1} \operatorname{Si}((n-2k)\pi),$$

Answer 3

Still not an answer

Using integration by parts, we are left with $$I=\pi \log (\pi )-\int_0^\pi \frac{x (1-\cos (x))}{x-\sin (x)}\,dx$$ $$\frac{x (1-\cos (x))}{x-\sin (x)}=\frac 1{\pi-2}\sum_{n=0}^\infty a_n \, \left(\frac{2 x-\pi }{2 \pi -4} \right)^n$$ where the first coefficients are $$\left( \begin{array}{cc} n & a_n \\ 0 & \pi \\ 1 & -8-4 \pi +2 \pi ^2 \\ 2 & 64-8 \pi -4 \pi ^2 \\ 3 & -320+\frac{128 \pi }{3}+32 \pi ^2-\frac{4 \pi^4}{3} \\ 4 & \frac{5120}{3}-\frac{992 \pi }{3}-240 \pi ^2+\frac{152 \pi ^3}{3}+\frac{4 \pi ^4}{3} \\ \end{array} \right)$$

If $$J_n=\int_0^\pi \left(\frac{2 x-\pi }{2 \pi -4} \right)^n\,dx$$ the odd terms are $0$ and $$J_{2n}=\frac\pi{2^{2 n}\, (2 n+1) }\,\left(\frac{\pi }{\pi -2}\right)^{2n}$$

For successive orders of the expansion, converting to decimals, we have $$\left( \begin{array}{cc} n & \text{approximation} \\ 0 & -5.04919444163 \\ 2 & -4.78383840146 \\ 4 & -4.78446883929 \\ 6 & -4.78466139402 \\ 8 & -4.78467018069 \\ 10 & -4.78467030234 \\ 12 & -4.78467028999 \\ 14 & -4.78467028892 \\ 16 & -4.78467028888 \\ 18 & -4.78467028888 \\ 20 & -4.78467028888 \\ \end{array} \right)$$

What we could also do is to use the $[n,n]$ Padé approximant built around $x=\frac \pi 2$ and, after converting the explicit result to decimals, obtain $$\left( \begin{array}{cc} n & \text{approximation} \\ 1 & -4.73316552793 \\ 2 & -4.78446723999 \\ 3 & -4.78467630069 \\ 4 & -4.78467042107 \\ 5 & -4.78467028782 \\ 6 & -4.78467028888 \\ \end{array} \right)$$