$\require{cancel}$ I am struggling with this integral:
$$\boxed{I = \int_{-\infty}^{+\infty} \dfrac{k\cdot \sin(kr)}{k^2-k_0^2}dk}$$
I’ll try to explain what I’ve done, hoping it’s correct. I started by rewriting the sine function in terms of the exponential function, using the relationship:
$\sin(x)= \dfrac{e^{ix}−e^{−ix}}{2i}$
To ensure the equivalence between the two equations, I then took the imaginary part of the expression.
$I = \text {Im}\left[\displaystyle\int_{-\infty}^{+\infty} \dfrac{k\cdot e^{ikr}}{k^2-k_0^2}dk\right]$
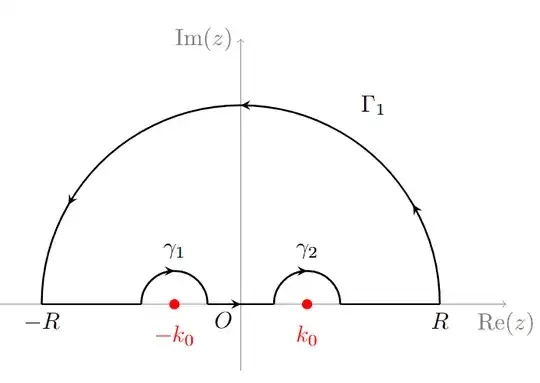
I chose a semicircle in the upper half. Was this obligatory? Because for example I learned that if I have a function of the type $\displaystyle \int_{-\infty}^{+\infty} f(x) e^{ikx} dx$ with $k>0$ then I must take the contour in the upper half-plane otherwise the integral diverges, but I don't know if this is also the case here. Anyway: the semicircular arc of the chosen contour vanishes by Jordan's lemma. Right? However, the function has two poles on the real axis and the integral diverges as we approach them. To solve this problem, we introduce two small arcs centred at the poles and take the limit for the radius which reduces to zero. In this way we are introducing the concept of principal value?
Drawing of the contour of the integral I chose and thanks to which the result came back:
Regardless, I defined a complex function $f(k)$ and found its poles.
$f(k) = \dfrac{k\cdot e^{ikr}}{k^2-k_0^2}dk$
The function has two simple poles at: $k^2-k_0^2=0 \implies k = \pm k_0$
For each pole, I calculated the residue using the standard formula: $\begin{align*} \mathop{\mathrm{Res}}_{k = k_0} \ f(k) = \lim_{k \to k_0} \dfrac{k\cdot e^{ikr}}{\cancel{(k-k_0)}(k+k_0)}\cdot \cancel{{(k-k_0)}} = \dots=\dfrac{e^{ik_0r}}{2} \end{align*}$
$\begin{align*} \mathop{\mathrm{Res}}_{k = -k_0} \ f(k) = \dots=\dfrac{e^{-ik_0r}}{2} \end{align*}$
My professor mentioned (or at least this is what I understood) that when we indent the contour around poles, we need to account for a "half residue." This means that instead of applying the Cauchy residue theorem in its usual form:
Cauchy residue theorem in its usual form:
$\displaystyle \oint_{\Gamma_1} f(k) dk = 2\pi i \sum \ \text{Res}(f(k))$
we instead have:
$\displaystyle \oint_{\Gamma_1} f(k) dk = \pi i \sum \ \text{Res}(f(k))$
In this way, I found a result that matched the one obtained by my professor. Is it a coincidence or did I do the exercise correctly? We will find out.
$\displaystyle \oint_{\Gamma_1} f(k) dk = {\displaystyle\pi i\cdot \sum \operatorname {Res} (f(k),\pm k_0)}= \pi i\left[\dfrac{e^{ik_0r} + e^{-ik_0r}}{2}\right] = \pi i \cos(k_0 r)$
$\implies I= \text{Im} \left[\displaystyle \oint_{\Gamma_1} f(k) dk\right] = \text{Im} \left[\pi i \cos(k_0 r)\right] \boxed{= \pi \cos(k_0 r)}$
Thank you very much for your attention and time.
Curiosity: could I have also used an outline of this kind? Because I tried, but it doesn't come :(
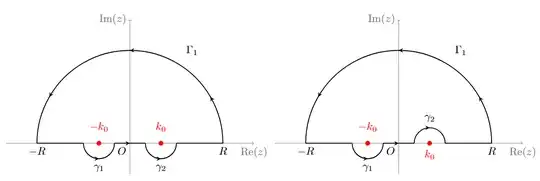
$$...$$instead of$\displaystyle...$. – emacs drives me nuts Jan 21 '25 at 19:56