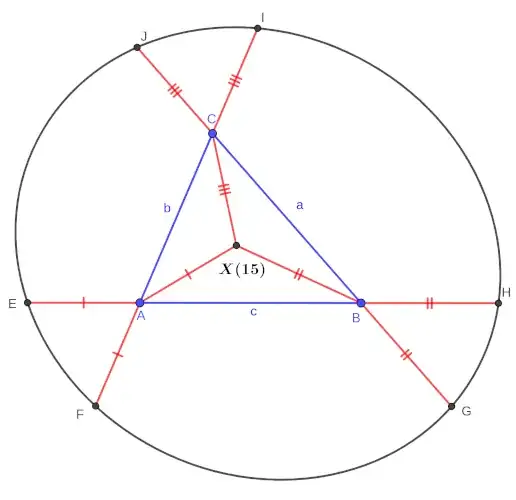
Can someone give me a hint on how to prove the following claim:
Given an arbitrary triangle $ABC$ with the first isodynamic point $X(15)$ . Extend the sides meeting at each vertex by the corresponding distance between the 1st isodynamic point and the vertex, the six endpoints of the three resulting line segments lie on an ellipse.
Generally, if the sides of the triangle are extended at vertices $A$, $B$, $C$ by lengths $a'$, $b'$, $c'$, one can show (I did it with a coordinate bash in Mathematica) that the endpoints lie on a conic if $$ (a - a') (bb' - cc')\;+\; (b - b') (cc' - aa') \;+\; (c - c') (a a' - b b') \;=\;0 \tag1$$ One can also show $$a\,|AX_{15}|=b\,|BX_{15}|=c\,|CX_{15}| \tag2$$ Taking $a' := |AX_{15}|$, etc, gives $aa'=bb'=cc'$, satisfying $(1)$. $\square$
Note: Taking $a'=a$, etc, also satisfies $(1)$. Moreover, the Conway Circle Theorem implies that the resulting conic is a circle. Taking $a-a'=b-b'=c-c'$ gives the Generalized Conway Circle Theorem.
