1

Chapter II, Exercise 102 of Besant's Conic Sections Treated Geometrically:

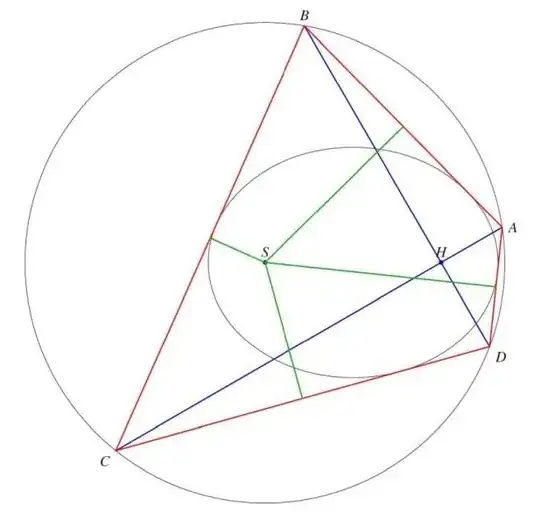
If an ellipse be inscribed in a quadrilateral so that one focus is equidistant from the four vertices, the other focus must be at the intersection of the diagonals.

His solution (hint) is:

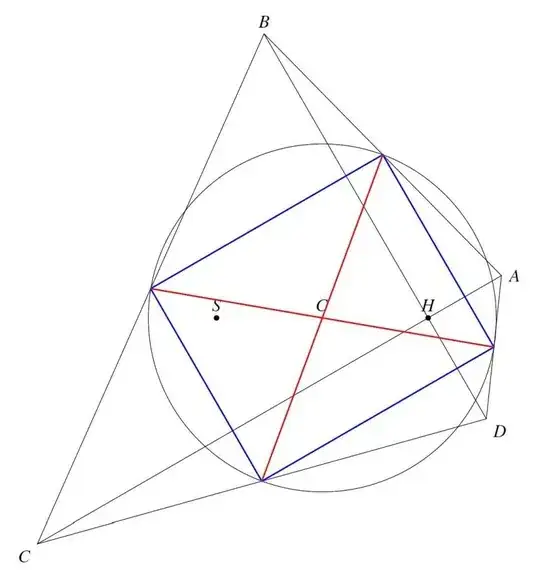
Dropping perpendiculars from the focus on the sides, their feet are the middle points, and, as they lie on a circle, form a rectangle; the diagonals, intersecting in H, are therefore at right angles, and SAD can be proved equal to HAB.

By constructing a circle centered on the first focus S, I get the locus of points equidistant from S. I see that the feet of the perpendiculars from S are the middle points and by experimenting I found that they lie on a circle centered at the center of the ellipse, but I don't know how to justify that. Since they are on the circle, they form a rectangle, but I don't see how this can be related to the diagonals and the second focus H. Attached are some figures I generated.

Besant's book is entirely based on Euclidean geometry, so I'm not interested in analytic solutions, etc.

enter image description here enter image description here

Intelligenti pauca
  • 55,765
Moti
  • 115
  • 7
  • Is there any reason why the diagonals must be perpendicular? $\quad$ The midpoints of a quadrilateral form a parallelogram. You can show that each edge is parallel to a diagonal (similar triangles, expansion ratio of 2). If the diagonals are perpendicular, then the midpoints form a rectangle. – Calvin Lin Jan 13 '25 at 15:30
  • I actually did get a rectangle with perpendicular diagonals (second diagram). Why Besant didn't ask for this explicitly in the statement of the exercise I don't know. Nor do I know why he is proving that the two angles are equal. – Moti Jan 13 '25 at 16:21
  • I can understand why he wants to prove those angles are equal: from that it follows that $H$ is the other focus, by the isogonal property. But I can prove the middle points are concyclic only by knowing in advance the diagonals are perpendicular, while Besant suggests the converse implication. – Intelligenti pauca Jan 13 '25 at 19:21

0 Answers0