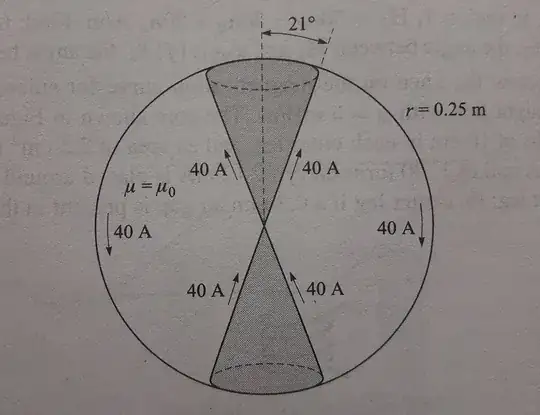
There are two conical sheets inside a sphere of radius r. The cones are hollow and exactly same. The spherical surface is cut at two places by the circular portion of the cones. How to calculate area of a part of the spherical surface excluding the parts cut by the cones as shown in the image? The cones subtend an angle of $21^°$ with their axis as shown.Height of each cone is equal to radius of the spherical surface.
$$Fig.1 - Two\ dimensional\ view\ of\ the\ spherical\ surface.$$
Is there any measure like a solid angle (in 3D) which can be estimated for the part of the spherical surface compared to a full cylindrical surface with area $4πr^2$ and thus the area of part of the spherical surface excluding the cones can be calculated ? Please suggest any techniques.
Reference: Engineering electromagnetics ,Hayt and buck, 8e, Mcgrawhill india, 2014, Fig.9-18,page 268