Growth rate of $\lim_{k\to\infty} \int_0^{\pi/2}\left| \frac{\sin(2kx)}{\cos(x)}\right|\,dx$

Question

Let $k\in\mathbb{N}$. Originally, I was looking at a similar limit:

$$\lim_{k\to\infty} \left|\int_0^{\pi/2} \frac{\sin(2kx)}{\cos(x)}\,dx\right|$$

Using induction and angle-addition, one can show

$$\sin(2kx) = 2(-1)^k \cos(x) \sum_{j=1}^{k}(-1)^j\sin((2j-1)x)$$

It follows that

$$\lim_{k\to\infty} \left|\int_0^{\pi/2} \frac{\sin(2kx)}{\cos(x)}\,dx\right| = \lim_{k\to\infty}2\sum_{j=1}^{k}\frac{(-1)^{j+1}}{2j-1} = \frac{\pi}{2}$$

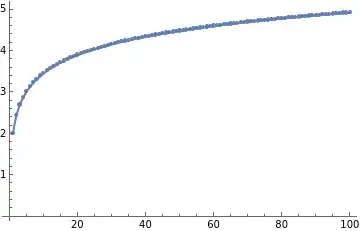
However, the limit obtained by moving the absolute values inside, i.e. $\lim_{k\to\infty} \int_0^{\pi/2} \left|\frac{\sin(2kx)}{\cos(x)}\right|\,dx$, is more interesting. For starters, I don't think it converges, though I can't show this at the moment. Empirically, the data are fit quite well by $f(k)=0.639135\log(1+22.326298k)$

We can't use the Dominated Convergence Theorem, as $\lim_{x\to\pi/2}|\sin(2kx)/\cos(x)|=2k$, so there's not a $g(x)$ that dominates $|\sin(2kx)/\cos(x)|$ on $[0,\pi/2]$. I also tried splitting $[0,\pi/2]$ into $k$ subsections, since we can still use the series identity, but that didn't seem to help with the integration. Perhaps differentiating under the integral sign will help?

Answer 1

The following analysis is inspired by Example 8 in Chapter I of the book Asymptotic Approximations of Integrals by R. S. C. Wong. First, note that $$ \int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} = \int_0^{\pi /2} { {\frac{{|\sin (2nx)|}}{{\sin x}}} {\rm d}x} . $$ Next, using the Fourier series $$ \left| {\sin x} \right| = \frac{2}{\pi } - \frac{4}{\pi }\sum\limits_{k = 1}^\infty {\frac{{\cos (2kx)}}{{4k^2 - 1}}} = \frac{8}{\pi }\sum\limits_{k = 1}^\infty {\frac{{\sin ^2 (kx)}}{{4k^2 - 1}}} , $$ we deduce $$ \int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} = \frac{8}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}\int_0^{\pi /2} {\frac{{\sin ^2 (2nkx)}}{{\sin x}}{\rm d}x} } . $$ Since $$ \frac{{\sin ^2 (jx)}}{{\sin x}} = \sum\limits_{m = 1}^j {\sin ((2m - 1)x)} , $$ we obtain $$ \int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} = \frac{8}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}\sum\limits_{m = 1}^{2nk} {\frac{1}{{2m - 1}}} } . $$ Now, we employ the asymptotic expansion $$ \sum\limits_{m = 1}^N {\frac{1}{{2m - 1}}} \sim \frac{1}{2}\log N + \frac{\gamma }{2} + \log 2 + \sum\limits_{j = 1}^\infty {\frac{{( 2^{2j - 1} -1)B_{2j} }}{{2^{2j+1} j }}\frac{1}{{N^{2j} }}} $$ and the identity $$ \frac{1}{2} = \sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}} , $$ to obtain \begin{align*} \int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} \sim\; & \frac{2}{\pi }\log n + \frac{2}{\pi }\left[ {\gamma + 3\log 2 + 2\sum\limits_{k = 1}^\infty {\frac{{\log k}}{{4k^2 - 1}}} } \right] \\& + \frac{8}{\pi }\sum\limits_{j = 1}^\infty {\frac{{( 2^{2j - 1}-1 )B_{2j} }}{{2^{2j+1}j }}\frac{1}{{n^{2j} }}\sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}} \frac{1}{{(2k)^{2j} }}} . \end{align*} Here $\gamma$ is the Euler–Mascheroni constant and $B_j$ are the Bernoulli numbers. Observe that $$ \sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}} \frac{1}{{(2k)^{2j} }} = \sum\limits_{k = 1}^\infty {\left( {\frac{1}{{4k^2 - 1}} - \sum\limits_{r = 1}^j {\frac{1}{{(2k)^{2r} }}} } \right)} = \frac{1}{2}\left( {1 + \sum\limits_{k = 1}^j {\frac{{( - 1)^k }}{{(2k)!}}B_{2k} \pi ^{2k} } } \right). $$ Thus, $$\boxed{ \int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} \sim \frac{2}{\pi }\log n + C + \sum\limits_{j = 1}^\infty {\frac{{A_j }}{{n^{2j} }}} } $$ as $n\to+\infty$, where $$ C = \frac{2}{\pi }\left[ {\gamma + 3\log 2 + 2\sum\limits_{k = 1}^\infty {\frac{{\log k}}{{4k^2 - 1}}} } \right] =1.99546621\ldots,$$ and $$A_j = \frac{2}{\pi }\left( {1 + \sum\limits_{k = 1}^j {\frac{{( - 1)^k }}{{(2k)!}}B_{2k} \pi ^{2k} } } \right)\frac{{(2^{2j - 1} - 1)B_{2j} }}{{2^{2j} j}}. $$

Answer 2

Here is a rather elementary way to show that indeed the sequence of integrals in the OP diverges:

Let $0<\alpha<1$. The function $x\mapsto |\sin 2x|$ is $\pi/2$-periodic; hence, by Fejér's lemma $$\int^{\pi/2}_0\frac{|\sin 2n x|}{\cos x}\,dx\geq\int^{(1-\alpha)\pi/2}_0\frac{|\sin 2n x|}{\cos x}\,dx\xrightarrow{n\rightarrow\infty}\Big(\frac2{\pi}\int^{\pi/2}_0|\sin 2x|\,dx\Big)\int^{(1-\alpha)\pi/2}_0\frac{dx}{\cos x}$$ as $\int^{\pi/2}_0\frac{dx}{\cos x}=\infty$, it follows from monotone converges that $$\int^{\pi/2}_0\frac{|\sin 2n x|}{\cos x}\,dx\xrightarrow{n\rightarrow\infty}\infty$$

---

I just noticed that the sequence of integrals in the OP is somewhat similar to the $L_1$ norm of the Dirichlet kernel in $\mathbb{S}^1$:

$$\mathcal{D}_n(x):=\frac{1}{2\pi}\sum_{|k|\leq n} e^{ink}=\frac1{2\pi}\frac{\sin\big((n+\tfrac12)x\big)}{\sin(x/2)}$$

It is known that $$\|\mathcal{D}_n\|_{L_1(\mathbb{S}^1)}=\frac1{\pi}\int^{\pi}_0\frac{|\sin\big((2n+1)x/2\big)|}{\sin x/2}\,dx\sim\frac{4}{\pi^2}\log n $$

---

Rather pedestrian and crude asymptotics can be obtain as follows:

Over $[0,\pi/2]$, we have $\frac{\sin x}{x}\geq \frac2\pi$

\begin{align} \int^{\pi/2}_0\frac{|\sin 2n x|}{\cos x}\,dx&=\int^{\pi/2}_0\frac{|\sin 2nx|}{\sin x}\,dx \\ &\leq\frac{\pi}{2}\int^{\pi/2}_0\frac{|\sin 2 nx|}{x}\,dx=\frac{\pi}2\int^{\pi n}_0 \frac{|\sin x|}{x}\,dx=O(\log n) \end{align}

Also, \begin{align} \int^{\pi/2}_0\frac{|\sin 2nx|}{\sin x}\,dx &\geq\int^{\pi/2}_0\frac{|\sin 2 nx|}{x}\,dx\\ &=\int^{\pi n}_0 \frac{|\sin x|}{x}\,dx=O(\log n) \end{align}

---

Answer 3

Sarting from @Gary's answer $$I_{n}=\int_0^{\pi /2} {\left| {\frac{{\sin (2nx)}}{{\cos x}}} \right|{\rm d}x} = \frac{8}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{{4k^2 - 1}}\sum\limits_{m = 1}^{2nk} {\frac{1}{{2m - 1}}} }$$

$$I_n=\frac 4 \pi\sum\limits_{k = 1}^\infty \frac{\psi \left(2 k n+\frac{1}{2}\right)-\psi \left(\frac{1}{2}\right)}{4 k^2-1}$$ $$I_n=\frac 4 \pi\sum\limits_{k = 1}^\infty \frac{\psi \left(2 k n+\frac{1}{2}\right)}{4 k^2-1}+\frac{2 (\gamma +2 \log (2))}{\pi }$$ If $n$ is large $$\psi \left(2 k n+\frac{1}{2}\right)=\log ( k)+\log (2n)+\frac{1}{96 k^2 n^2}-\frac{7}{15360 k^4 n^4}+O\left(\frac{1}{n^6}\right)$$ $$\sum\limits_{k = 1}^\infty \frac{\psi \left(2 k n+\frac{1}{2}\right)}{4 k^2-1}=\frac{1}{2} \log (2 n)+\frac{12-\pi ^2}{576 n^2}+\frac{7 \left(-720+60 \pi ^2+\pi ^4\right)}{1382400 n^4}+\sum _{k=1}^{\infty } \frac{\log (k)}{4 k^2-1} $$

Since $$\int \frac{\log (k)}{4 k^2-1}=\frac{1}{4} (-\text{Li}_2(1-2 k)-\text{Li}_2(-2 k)-\log (2) \log (1-2 k)-\log (k) \log (2 k+1))$$ we can use Euler-MacLaurin summation to obtain $$\sum _{k=1}^{\infty } \frac{\log (k)}{4 k^2-1}=C-\frac{\log (k)+1}{4 k}+\frac{\log (k)}{8 k^2}+O\left(\frac{1}{k^3}\right) $$ For this level of expansion $$C=\frac{1}{4}\text{Li}_2(-2)+\frac{\pi ^2}{16}-\frac{199961969}{165337200}$$ which is $0.391578$ while the infinite summation is $0.238907$.

$$I_n=\frac 2 \pi \log(n)+\frac{2 (2 C+\gamma +3 \log (2))}{\pi }+\frac{12-\pi ^2}{144 \pi n^2}+O\left(\frac{1}{n^4}\right)$$ The constant term is $2.18985$.

A few numbers for comparaison $$\left( \begin{array}{ccc} n & \text{approximation} & \text{integration}\\ 10^0 & 2.19456 & 2.00000 \\ 10^1 & 3.65577 & 3.46138 \\ 10^2 & 5.12160 & 4.92721 \\ 10^3 & 6.58747 & 6.31663 \\ 10^4 & 8.05334 & 7.85440 \\ 10^5 & 9.51921 & 9.39135 \\ \end{array} \right)$$