3

I want to evaluate the following integral using residue theorem and contour integration $$I(a) =\int_{-\infty}^{+\infty}\frac{e^{ax}}{1+e^{3x}}dx, \quad a\in \Bbb R$$

First we observe that $I(a)$ converges iff $a\in(0,3)$ and after some tries and calculation I think the best approach is use the following contour

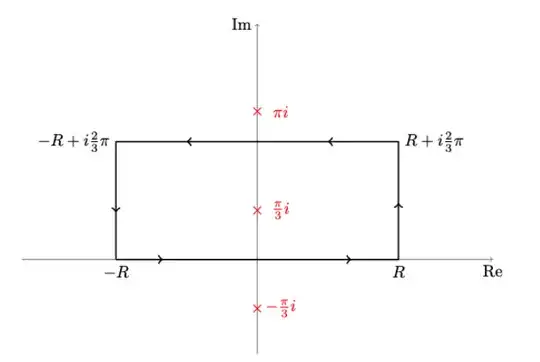
Contour 1

red are the poles of the function $f(z) = \frac{e^{az}}{1+e^{3z}}$, contour is chosen in order to take advantage of the periodicity of $e^{ix}$. If my calculation are correct the value for $a\in (0,3)$ should be

$$\boxed{I(a) = \frac{\pi}{3\sin\left(\frac{\pi}{3}a\right)}}$$

This I think it's correct but it's my second attempt because (and here is the question) taking inspiration from other answers on the site

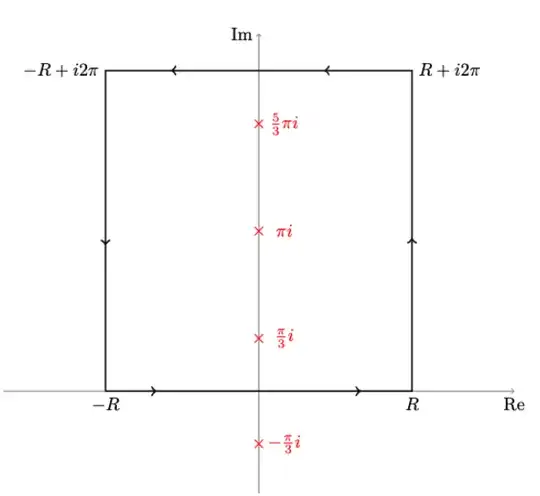
My original contour was bigger

Conntour 2

Here I got in trouble since from the upper part I get that the integral evaluated on the path is

$$\int_{R}^{-R} f\left(x+i2\pi\right)dx = -e^{i2\pi a}I(a)$$

(The equality holds when we pass to the limit $R\to \infty$, I beg everyone pardon...) this lead to trouble because than I get something like

$$\left(\color{red}{1-e^{i2\pi a}}\right)I(a) = 2\pi i\sum_{z_j \ \text{residue inside}\\ \text{the contour}} \text{Res}_f(z_j)$$

and for $a\in(0,3)$ the red term vanish for example for $a=1,2$. In the end my question in since changing the contour should get me to the same result I think why does this happen, is there something that let this contour forbidden? I get the feeling that maybe it's something involving the holomorphycity of the function $f$.

Thank you for the help!

Turquoise Tilt
  • 2,571
  • "This leads to trouble because then I get something like:" - why is this trouble? You haven't shown your computation of the residues. Did you really get a different answer? Both methods will work – FShrike Jan 02 '25 at 22:28
  • @FShrike I’ll double check my calculation but I don’t remeber if whit $a=1,2$ the integral is zero – Turquoise Tilt Jan 02 '25 at 23:15

1 Answers1

-1

After double checking for $a=1$ as suggested in the comments $$\begin{align*} \text{Res}_f\left(\frac{\pi}{3}i\right) & = -\frac{\cos\left(\frac{\pi}{3}\right)+i\sin\left(\frac{\pi}{3}\right)}{3} \\ \text{Res}_f\left(\pi i\right) & = -\frac{\cos\left(\pi\right)+i\sin\left(\pi\right)}{3}\\ \text{Res}_f\left(\frac{5\pi}{3}i\right) & = -\frac{\cos\left(\frac{5\pi}{3}\right)+i\sin\left(\frac{5\pi}{3}\right)}{3} \end{align*}$$

And the sum of these three is equal to zero. Equally holds for $a=2$.

In conclusion the red term vanishes on LHS as RHS. This approach is less efficient since I could not evaluate the integral and I think the solution proposed before is a better way to handle the problem.

Turquoise Tilt
  • 2,571