A few years back I wrote some custom 2D graphics rendering code. To fill any shape, that shape supplies a scan(y) function which returns the left and right edge coordinates of the horizontal span(s) of the shape which intersect that scanline y coordinate. The horizontal spans are then filled in using the current drawing color or paint texture.
For an ellipse, its scan function has a pleasing mathematical basis: it solves the associated quadratic of the ellipse and returns the two roots of x for each y.
$$\dfrac {((x-h)\cos(A)+(y-k)\sin(A))^2}{a^2}+\dfrac{((x-h) \sin(A)-(y-k) \cos(A))^2}{b^2}=1$$
It's much faster than converting the ellipse to a polygon and finding horizontal spans with generic edge scanning techniques. I'm using this for interactive display of a lot (thousands) of spheres, so speed matters to me, although I also want to keep the implementation simple.
To also draw the outlines of some basic shapes, I use boolean subtraction: subtract a smaller version of the shape from a bigger version. Here is how I produce a scan function for an outlined ellipse (slightly paraphrased):
static Scanner outlineEllipse(float centerX, float centerY, float radiusA, float radiusB, float angle, Stroke stroke) {
float hl = stroke.getLineWidth() * 0.5f;
return subtract(
fillEllipse(centerX, centerY, radiusA + hl, radiusB + hl, angle),
fillEllipse(centerX, centerY, radiusA - hl, radiusB - hl, angle));
}
Here, fillEllipse returns a scan(y) function for filling an ellipse, and subtract combines the results of two such functions. You see I'm simply adding or subtracting half the stroke width to the ellipse radiuses.
I was perfectly happy with this. It's fast and easy and it worked for everything I tested.
Today I noticed some that in certain cases the outlines looked a little odd.
I set up a test, drawing a series of ellipses with a thick black outline:
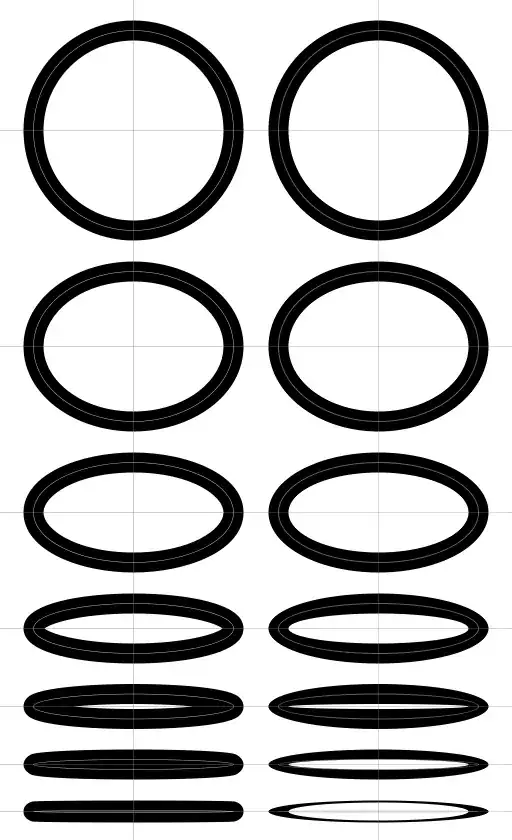
On the left are outlined ellipses drawn by a traditional graphics library, correctly. (The faint white line inside each thick black line shows the underlying ellipse, before outlining.)
On the right are the same outlined ellipses drawn by my graphics code. The top one, a circle, is perfect, but the more eccentric the ellipse, the more wrong and ugly it gets.
So now I realize, the shape of an outlined ellipse is not an ellipse. Neither the outside nor the inside shape. I had absolutely never imagined this until I saw it.
So I am wondering, what shape is it?
I have been trying to come up with some description for what the outline should really do: it inflates or deflates the shape by offsetting its edge by a distance of half the stroke thickness, in a direction perpendicular to the edge. The ideal outline should have a constant thickness.
Is there any mathematical function for such an "inflated" or "deflated" ellipse? Hopefully something reasonably friendly to solve like the ellipse quadratic?