While running some code, I saw this post asking on how to graph a functional. I've been thinking about the subject myself, and how to do some nice visualizations of function spaces (and some associated functional).
The author of that post wanted an answer, so I thought I'd go ahead with my ideas and take a crack at drawing out not only the graph of a simple function space, but also the graph of a functional defined on it.
I'm going to use a very simple toy function space, but I feel you can easily extrapolate off of what I've written.
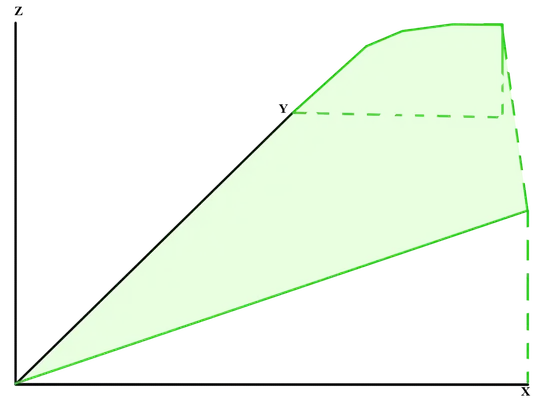
Graph of Function Space:
Formally, denote the space of all smooth functions on the unit interval by $\text C^\infty [0,1]$.
We know that we can have an indexed family of functions $f_y: [0, 1] \rightarrow \mathbb R $ that every function in our space is part of. We can choose to have indexed functions be ones that we are well acquainted with. For instance, we can have $f_0 (x) = x$ and then have $f_1(x) = \sin (x)$. We can choose to have all intermediate functions be given by a straight-line homotopy.
Consequently, the graph of our function space will be given by all points $\left(x, y, f_y(x) \right)$.
Practically, we'll only be able to draw out a finite number of functions and the straight-line homotopies between them, but this isn't any different than only being able to draw a function of form $\mathbb R \rightarrow \mathbb R$ on a small "slice" of its domain.
We can draw this "slice" of our graph as a family of green curves, which due to the homotopy between them resembles a kind of surface:
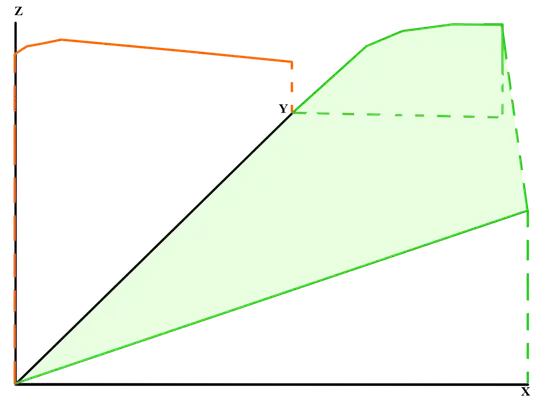
Graph of Functional:
The graph of the functional $\omega: \text C^\infty [0, 1] \rightarrow \mathbb R$ is extremely easy to define. It is all points $\left(0, y, \omega(f_y) \right)$. We can draw this graph as an orange curve. Drawing directly on top of the "slice" of our previous construction, we can obtain a picture that looks something like this:
Has this been done before? Are there other methods that draw the graph of a functional out? I feel like this is a nice toy for visualizing things like extremals and variational methods, either through a static picture or an animation.