0

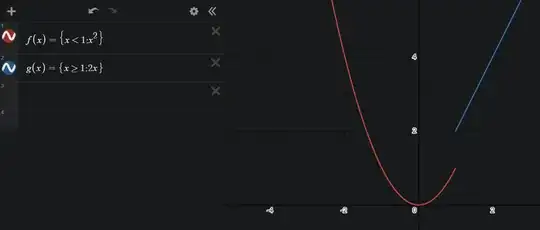
Let's say I have the following function

$f(x)=\begin{cases} x^2 & x < 1, \\ 2x & x \geq 1 \end{cases}$

$f'(x)=\begin{cases} 2x & x < 1, \\ 2 & x > 1 \end{cases}$

$\implies \lim_{x\to 1^{-}}f'(x)=2$ and $\lim_{x\to 1^{+}}f'(x)=2$

I know that I can't conclude $f'(1)=2$ from here as it would require assuming continuity of $f'(x)$.

My first question is" Is $\lim_{x\to 1^{-}}f'(x)=2$ same as saying LHD at $x=1$ is $2$ and in which cases it is true as many questions can be solved directly by assuming this"

Let's calculate LHD and RHD from their definition

$$\text{LHD}= \lim_{x \to 1^{-}} \frac{x^2-2}{x-1}= \infty$$ $$\text{RHD}= \lim_{x \to 1^{+}} \frac{2x-2}{x-1}= 2$$

It is apparent that what I am thinking is clearly wrong for the LHD atleast, but I can't seem to find the answer myself.

Also drawing the graph increases my confusion as it seems that LHD is indeed $2$

My second question is "why the intuitive geometric slope from the graph contradicts with LHD being infinite?"

enter image description here

user6262
  • 1,200
  • 2
    You need $f$ to be continuous from the left at $x=2$, otherwise the derivative from the left at that point can't possibly exist. But if that's the case, then you can draw the desired conclusion: https://math.stackexchange.com/questions/257907/prove-that-fa-lim-x-rightarrow-afx – Hans Lundmark Dec 09 '24 at 21:37
  • @Hans Lundmark Why it does not work here despite satisfying all conditions

    $f(x)=\begin{cases} x^2 sin(\frac{1}{x})& x \neq 0, \ 0 & x=0 \end{cases}$

    It is both righ tand left continuous at $x=0$

    LHD=RHD=$0$ at $x=0$(Using definition)

    $f'(x)=2x sin(\frac{1}{x})-cos(\frac{1}{x})$ for $x\neq0$

    $lim_{x\to 0} f'(x)$ does not exist but LHD=RHD=$0$

     – user6262 Dec 09 '24 at 23:00
  • That example doesn't satisfy the condition that $f'(x)$ has a limit to begin with. – Hans Lundmark Dec 10 '24 at 05:18
  • 1
    The hypothesis in the linked discussion is that the limit of the derivative exists. If so, that’s the derivative at the point. – Ted Shifrin Dec 10 '24 at 05:22

1 Answers1

1

There's a theorem that states:

Let $f:[a,b)\to\mathbb{R}$, continuous in $[a,b)$, derivable in $(a,b)$ and $\displaystyle\exists\lim_{x\to a^+}f'(x)=m\in\mathbb{R}$, then $f'_+(a)=m$

I think you are confusing the right limit of the derivative $f'_+(a)$ with the RHD i.e. $\displaystyle\lim_{x\to a^+}\frac{f(x)-f(a)}{x-a}$, the two things are unrelated to each other (same for LHD).

So, answering your questions

Is $\displaystyle\lim_{x\to1}f′(x)=2$ same as saying LHD at $x=1$ is $2$

No, in your case it's the same as saying $f'_+(1)=f'_-(1)=2$, if $f'$ was defined in $1$.

At most you can say that $f'$ is extendable by continuity in $x=1$

and in which cases it is true

I think that to be true a sufficient condition is: $f$ is continuous in $x=1$ (more generally in $x=a$)

why the intuitive geometric slope from the graph contradicts with LHD being infinite?

Because for $x\ge 1$ your function is $f(x)=2x$, so $f(1)=2$.

Geometrically: imagine the tangent line in $x=1$, it must pass through $(1,2)$ and through $x^2$, i.e. it must pass through $(1,2)$ and approximately $(1,1)$, which is the slope of that line?

SwitchArio
  • 291