0

Let say the target rate is: $$ 0.2312076819339227309219662514224185 $$ How to adjust this fraction $984398920/4257639330$ that gives this $\mbox{rate}\ ?$: $$ 0.23120768193392275902336706383252993860332457986759 $$ ( matches the $16$th number after the floating point ) to match the $18$th number after the floating point ?. $$ \mbox{The final fraction is:}\quad {939515904 \over 4063515088} $$ Also the fraction parts should not exceed ${\tt 0xffffffff} \left(4200000000\right)$.

The problem is I didn't know how to adjust it to know if I'm close to the exact rate ( $18$th number ) or not untill I get it, other says how will be the change ?.

RobinSparrow
  • 3,669
Benraouane Soufiane
  • 1
  • 2
  • 1
    Not entirely sure what you're getting at, but look up Continued Fractions perhaps. https://en.m.wikipedia.org/wiki/Continued_fraction – Benjamin Wang Dec 07 '24 at 15:26
  • If you use continued fractions you have guaranteed rapidest convergence to your true fraction and also bounds $\frac{1}{q^2}$ on each convergent distance from the desired value. – RobinSparrow Dec 07 '24 at 16:01
  • @BenjaminWang the initial fraction obtained by the continued fractions, but it does not gives the accurate rate at least match the 18th number within the interval limits (<4200000000) – Benraouane Soufiane Dec 07 '24 at 19:45
  • @RobinSparrow I'm using the reccurrence equation to calculate the numerator (also the same equation for the denominator) p_k = a_k p_{k-1} + p_{k-2} what should I add to apply what have you said please? – Benraouane Soufiane Dec 07 '24 at 19:57
  • You do that for both the numerator and denominator terms, $p$ and $q$, the bound is derived from the denominator. If you've not figured it out by tomorrow I'll post when I'm back near a computer. – RobinSparrow Dec 07 '24 at 20:04
  • This thread or this thread may help, – Raymond Manzoni Dec 09 '24 at 17:28
  • A similar question: https://math.stackexchange.com/questions/4388232/reduce-precision-of-fraction/ – awkward Dec 10 '24 at 14:01
  • @RaymondManzoni I've checked them, does not resolve what I'm asking for – Benraouane Soufiane Dec 11 '24 at 15:35
  • Well $$0.2312076819339227309219662514224185= [0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 5, 1, 1,\cdots]$$ while $$0.23120768193392275902336706383252993860332457986759\approx [0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 9]$$ so that you could replace the final $9$ by $5$ to get $$[0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 5]=58719744/253969693=939515904/4063515088$$ (or replace $9$ by $5,1$ or $5,1,1$ and so on until getting the wished precision without exceeding the DWORD limit). – Raymond Manzoni Dec 11 '24 at 16:33
  • This was written because you seem wanting to adjust $984398920/4257639330$ to get your initial value (with the plan of evaluating both continued fractions in parallel until obtaining different terms). The idea of my other answer was to search directly the continued fraction for your initial value (see the comments). – Raymond Manzoni Dec 11 '24 at 16:59
  • @RaymondManzoni can you tell me how do you get the 587.../253... The equation of calculating the numerator & denominator? It seems the problem not with the continued fraction coefficients because I started with the correct one (coefficients of target rate) – Benraouane Soufiane Dec 12 '24 at 16:27
  • @BenraouaneSoufiane: The successive fractions $\frac {A_n}{B_n}$ are obtained using the recurrence relation for continued fractions :\begin{align} A_n &= b_n A_{n-1} + A_{n-2}, \ B_n &= b_n B_{n-1} + B_{n-2} \qquad \text{for } n \ge 1 \end{align} (since $a_n=1$ for simple fractions) – Raymond Manzoni Dec 12 '24 at 16:40
  • this should return the successive fractions : $$\frac 01,\frac 14,\frac 3{13},\frac {40}{173},\cdots,\frac{58719744}{253969693}$$ \begin{align} 3&= 3 * 1+0\13&=3 * 4+1\end{align} – Raymond Manzoni Dec 12 '24 at 16:45
  • This was provided too by RobinSparrow in his answer (+1) – Raymond Manzoni Dec 12 '24 at 16:54
  • @RaymondManzoni I'm using the same equations which gives 98439892/425763933 instead 58719744/253969693 what's wrong for you? – Benraouane Soufiane Dec 12 '24 at 17:38
  • Remember that the $9$ at the right had to be replaced by $5$ :\begin{align} [0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 9]=\dfrac{98439892}{425763933}\ [0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 5]=\dfrac{58719744}{253969693}\end{align} – Raymond Manzoni Dec 12 '24 at 18:14
  • @RaymondManzoni it works! So the problem with my function, does not return the correct continued fractions coefficients, but it gives the correct one until the term 16, what's wrong for you? – Benraouane Soufiane Dec 12 '24 at 18:58
  • @BenraouaneSoufiane: I will only guess that your problem came from your use of double precision to evaluate the c.f. : you were probably not computing the c.f. of your initial value but rather of something near 0.23120768193392276 (the 53-bit rounded value from the mantisse limitation of double precision). Quadruple precision (if available) could help you to get more terms. Fine continuation anyway, – Raymond Manzoni Dec 12 '24 at 21:40
  • @RaymondManzoni How to mark this question as answered/resolved (by your comments)? – Benraouane Soufiane Dec 13 '24 at 15:30
  • @BenraouaneSoufiane: my comments did not answer directly your initial question but you may answer yourself to clarify all this (and accept your answer) or update/clarify your question and accept RobinSparrow's answer. – Raymond Manzoni Dec 13 '24 at 16:15

1 Answers1

1

If you ask Wolfram to convert your target rate of: $$0.2312076819339227309219662514224185$$ to continued fractions it returns a series of partial quotients $a_i$: $$[0, 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 5, 1, 1, 1, 2, 1, 5, 1, 1, 11, 3, 10, 4, 3...]$$ and if you then ask for the convergents $\frac{p_i}{q_i}$ derived from this series we obtain a series of fractions $$[\frac{0}{1}, \frac{1}{4},\frac{3}{13},\frac{40}{173}...]$$ and assuming you require $p+q<4200000000$ you could take later terms like the $21$st: $$\frac{715427443}{3094306543}$$ which will deviate from your desired value by less than $$\frac{1}{3094306543^2}$$ which I believe should already be sufficient as it is near $10^{-20}$.

Edit 1: to show commands and the list of fractions:

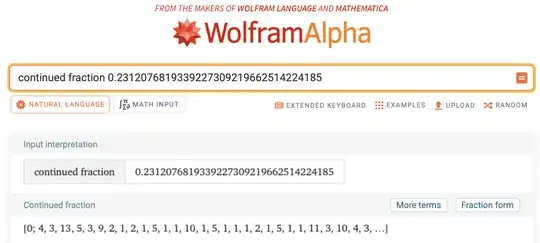
enter image description here

And in the list below, the one I reference is the 21st, neglecting the leading term of zero.

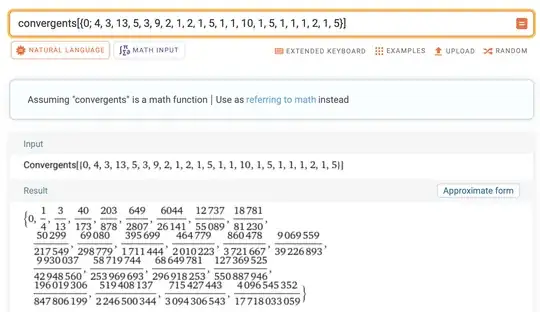
enter image description here

Edit 2: to describe CF algorithm for convergents for OP.

Given a sequence of partial quotients $a_i$ we obtain convergents with numerators $p_i$ and denominators $q_i$ via the recurrence relation $p_i=a_ip_{i-1}+p_{i-2}$ and similarly for $q_i$ with initiating terms $p_{-1}=0, p_0=1,q_{-1}=1,q_o=0$.

$p_1=a_1p_0+p_{-1}=a_1\times1+0=a_1$

$p_2=a_2p_1+p_0=a_2a_1+1$, etc.

Concretely, with $a_i:[0,4,3,13,5,...]:\\ p_1=0 \times 1 + 0 = 0\\ p_2=4 \times 0 + 1 = 1\\ p_3=3 \times 1 + 0 = 3\\ p_4=13 \times 3 + 1 = 40\\ p_5=5 \times 40 + 3 = 203$

And you should see how this matches the first several numerators output by WA in the screenshot above. The theory of how this works is not hard, the gentlest introduction I know of is Continued Fractions by CD Olds, targeting a high school audience.

Edit 3:

I see from further comments some confusion remained. And that I neglected to mention in my answer the key point I made in the comments. The key to immediately choosing the right fraction to represent your target with desired precision is that fractions produced by continued fractions (i.e., convergents) come with a guarantee that the error of a convergent $\frac{p_i}{q_i}$ is bounded above by $\frac{1}{q_i^2}$.

The initial rate and target rate are represented as decimals then continued fractions below:

$ 0.23120\ 76819\ 33922\ 75902\ 33670\ 63832\ 52993\ 86033\ 24579\ 86759 \\ 0.23120\ 76819\ 33922\ 73092\ 19662\ 51422\ 4185 \\ [0; 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 9] \\ [0; 4, 3, 13, 5, 3, 9, 2, 1, 2, 1, 5, 1, 1, 10, 1, 5, 1, 1, 1, 2, 1, 5, 1, 1, 11, 3, 10, 4, 3,...] $

These begin diverging at the 17th decimal place, and (coincidentally) the 17th partial quotient in continued fraction form.

Taking the continued fraction form, if we adjust the original 9 to a target 5 we obtain $\frac{p_{17}}{q_{17}}=\frac{58719744}{253969693}$ as the "best" adjustment of the original fraction. However, this only agrees to the 16th decimal place, not the requested 18th:

$ 0.23120\ 76819\ 33922\ 73092\ 19662\ 51422\ 4185 \\ 0.23120\ 76819\ 33922\ 72203\ 12464\ 60577 $

Which is sensible since the error is bounded by $\frac{1}{253969693^2} \approx 10^{-17}$. We must take the convergents further to obtain the needed precision, sequentially the next several yield the following decimals (target at top)

$ 0.23120\ 76819\ 33922\ 73092\ 19662\ 51422\ 4185 \\ 0.23120\ 76819\ 33922\ 73529\ 23971\ 29927 \\ 0.23120\ 76819\ 33922\ 72917\ 87575\ 25401 \\ 0.23120\ 76819\ 33922\ 73131\ 98732\ 57968 \\ 0.23120\ 76819\ 33922\ 73079\ 48277\ 79470 \\ 0.23120\ 76819\ 33922\ 73093\ 86845\ 06411 \\ $

These last two, accurate to the 18th place, correspond to $\frac{519408137}{2246500344},\frac{715427443}{3094306543}$, the latter being the one I mentioned initially in my answer. Both have terms summing to less than the needed size, and bounds on error of $\frac{1}{q_i^2} < 2*10^{-19}$, whereas all prior terms have bounds $>10^{-18}$, which is why none of them were satisfactory. The key is $\frac{1}{q_i^2}$.

RobinSparrow
  • 3,669
  • If I select the term 21 it gives huge fraction: 3042365112735/13158581441963 from what you get the fraction 715.../309... I found the 984.../425... (then I multiply both by ten) is the nearest to the 939.../406.... – Benraouane Soufiane Dec 09 '24 at 16:18
  • @BenraouaneSoufiane: see the pics from WolframAlpha added in an edit. The first few terms check out by hand, I do think WA is doing the arithmetic correctly, the term I was speaking about is the 21st if you don't count the zero up front, each $p,q$ can be obtained from the prior two recursively as, e.g., $p_i=a_ip_{i-1}+p_{i-2}$ with initiating terms $(0,1),(1,0)$ for $p,q$ respectively. – RobinSparrow Dec 09 '24 at 17:03
  • Thank you for your effort, although it gives accurate fraction rather than what I have provide, I don't know how pi & qi are calculated, even it matches the 19th numbers does not gives the needed fraction – Benraouane Soufiane Dec 11 '24 at 15:18
  • No problem. I don't fully understand your English and can't tell if you're saying the fraction mentioned is "good enough" or "not good enough". There is a nice introductory book to continued fractions, called Continued Fractions, by CD Olds, which presumes no prior knowledge and will teach you within the first chapter how they work. You can find used copies for a few dollars, it's an old book, and it's also an eBook for more. But I'll edit to show you how to do the calculations. – RobinSparrow Dec 11 '24 at 15:35
  • I'm doing the same, but it does not return what walframalpha returns, in reality it returns my initial fraction – Benraouane Soufiane Dec 12 '24 at 15:23
  • Yes it returns the fraction you mention as final, eventually. But I thought the whole point of this post was to find a fraction in lesser terms, but accurate to a desired precision, which is what I've tried to give you too. Whatever it is you actually need, I would use the continued fraction framework I've illustrated and that Benraouane has also highlighted. – RobinSparrow Dec 12 '24 at 17:33