Per Gary's comment below, substituting $x = \sinh t$ yields
$$I(\alpha) = \int_0^\infty \frac{e^{-\alpha \cosh t}}{\cosh t} \,dt .$$
This integral is a representation of the Bickley (or Bickley–Naylor) function $\operatorname{Ki}_1(\alpha)$ of order $1$; see DLMF $\S$10.43.12 and references therein. Alternatively, $I(\alpha) = \operatorname{Ki}_1(\alpha)$ can be expressed in terms of the Modified Bessel Function of the Second Kind, $K_m(\alpha)$, and the Modified Struve Functions, $L_m(\alpha)$.
To obtain asymptotics for $\operatorname{Ki}_1(\alpha)$, notice first that the form of the integral suggests differentiating under the integral sign w.r.t. $\alpha$, which yields
$$\operatorname{Ki}_1'(\alpha) = -\int_0^\infty e^{-\alpha \cosh t} \,dt = - K_0(\alpha), $$ so we can derive the asymptotics of $\operatorname{Ki}_1$ using those of $K_0$.
About $\alpha = 0$ we have
$$K_0(\alpha) \sim -\log \alpha + (\log 2 - \gamma) \alpha + \cdots ,$$
where $\gamma$ is the Euler–Mascheroni constant and $\cdots$ denotes terms of order $\alpha^2 \log \alpha$. Integrating and using that $\operatorname{Ki}_1(0) = \frac\pi2$ yields
$$\boxed{\operatorname{Ki}_1(\alpha) \sim \frac\pi2 + \alpha \log \alpha + (\gamma - 1 - \log 2) \alpha + \cdots} ,$$ where $\cdots$ denotes a remainder in $O(\alpha^2 \log \alpha)$ (in fact in $O(\alpha^3 \log \alpha)$).
Similarly, expanding $K_0$ at $\infty$ gives
$$K_0(\alpha) \sim \sqrt{\frac\pi{2 \alpha}}e^{-\alpha} \left(1 - \frac1{8\alpha} + \frac9{128 \alpha^2} + \cdots\right) ,$$
where $\cdots$ denotes a remainder in $O(\alpha^{-3})$. Integrating and using that $\lim_{\alpha \to \infty} \operatorname{Ki}_1(\alpha) = 0$ yields
$$\boxed{\operatorname{Ki}_1(\alpha) \sim \sqrt{\frac\pi{2 \alpha}}e^{-\alpha} \left(1 - \frac5{8 \alpha} + \frac{129}{128 \alpha^2} + \cdots\right)}, $$
where again $\cdots$ denotes a remainder in $O(\alpha^{-3})$. The leading term can alternatively be extracted by instead substituting $x = \tan \theta$ in the original integral, which yields $\operatorname{Ki}_1(\alpha) = \int_0^{\frac\pi2} e^{-\alpha \sec \theta} \,d\theta$, and applying Laplace's Method with $f(\theta) = -\sec \theta$.
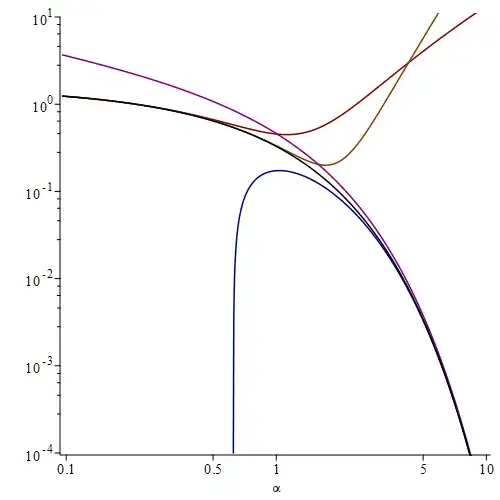
The function $\operatorname{Ki}_1(\alpha)$ and some of its asymptotic approximations
$$\left\{\begin{array}{l}
\operatorname{Ki}_1(\alpha) \\
\color{#7f0000}{\frac{\pi}{2} + \alpha \log \alpha + (\gamma - 1 - \log 2) \alpha} \\
\color{#7f3f00}{\frac{\pi}{2} + \alpha \log \alpha + (\gamma - 1 - \log 2) \alpha + \frac1{12} \alpha^3 \log \alpha + \frac1{36} (3\gamma - 4 - 3 \log 2) \alpha^3} \\
\color{#7f007f}{\sqrt{\frac\pi{2 \alpha}}e^{-\alpha}} \\
\color{#00007f}{\sqrt{\frac\pi{2 \alpha}}e^{-\alpha} \left(1 - \frac5{8\alpha}\right)}
\end{array}\right.$$
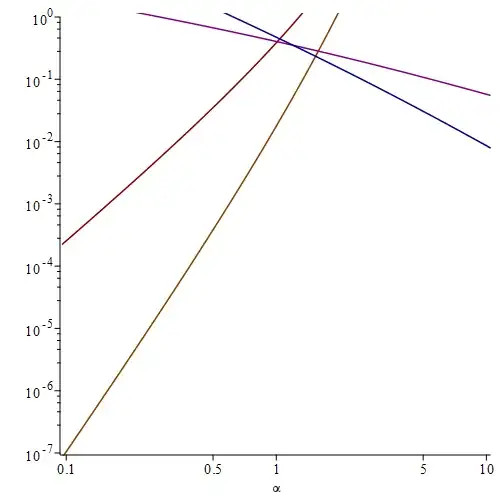
Relative errors of the asymptotic approximations
For $k \geq 0$,
$$I_k(\alpha)
= \int_0^\infty (1 + x^2)^{\frac{k - 1}2} e^{-\alpha \sqrt{1 + x^2}} \,dx = \int_0^\infty e^{-\alpha \cosh t} \cosh^k t \,dt = (-1)^k \frac{d^k}{d\alpha^k} K_0(\alpha) .$$
In particular, the integral $J(\alpha) := \int_{0}^{\infty} e^{-\alpha\sqrt{1 + x^2}}$ is $I_1(\alpha) = -K_0'(\alpha) = K_1(\alpha)$.
Differentiating the earlier series for $K_0$ gives for small $\alpha$ that
$$\boxed{K_1(\alpha) \sim \frac1\alpha + \frac12 \alpha \log \alpha + \frac14 (2 \gamma - 1 - 2 \log 2) + \cdots} ,$$
where $\cdots$ denotes a remainder in $O(\alpha^3 \log \alpha)$, and for large $\alpha$ that
$$ \boxed{K_1(\alpha) \sim \sqrt{\frac{\pi}{2\alpha}}e^{-\alpha} \left(1 + \frac{3}{8 \alpha} - \frac{15}{128 \alpha^2} + \cdots \right)} ,$$
where $\cdots$ denotes a remainder in $O(\alpha^{-3})$.

