When the exponent $\alpha$ is not an integer, defining $z^\alpha$ requires a choice: Explicitly, we pick a branch $\log$ of the logarithm and define $z^\alpha := \exp (\alpha \log z)$. For some choices the contour intersects the branch cut, in which case the Residue Theorem does not apply.
The integrand $\frac{1}{z^\alpha + 1}$ has a branch cut $\mathcal B$ where our choice of logarithm does, and its poles will be at the solutions of $\exp (\alpha \log z) = -1$, i.e., where $\alpha \log z = \pi i \ell$ for some odd integer $\ell$ (except of course for those solutions that lie on the branch cut itself).
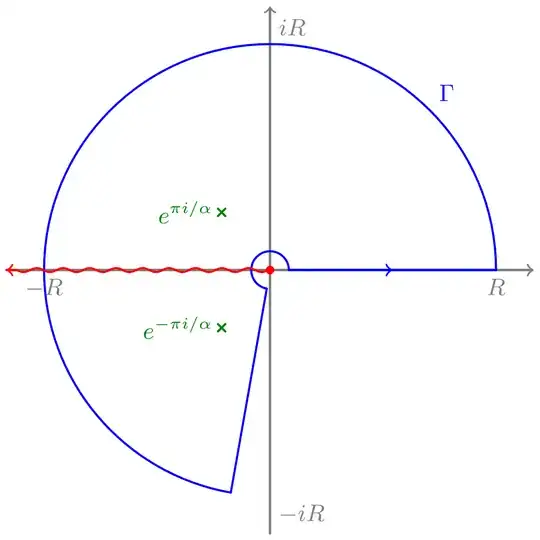
If we take the most common choice of $\log$, whose imaginary part takes values in, say, $(-\pi, \pi)$, then the integrand $\frac{1}{z^\alpha + 1}$ has a branch cut $\mathcal B$ along the negative real axis and has poles at $z = \exp \frac{\pi i \ell}\alpha$, where $\ell$ is an odd integer in $(-\alpha, \alpha)$. If $\alpha > 2$, then the slice contour $\Gamma$ (with its clockwisemost side along the positive real axis) is contained entirely inside the open, simply connected set $\Bbb C \setminus \mathcal B$ on which the integrand is meromorphic, and the Residue Theorem applies. If $\alpha \in (1, 2]$, however, then $\Gamma$ intersects $\mathcal B$ and the Residue Theorem does not apply.
Illustration: The case $\alpha \in \left(1, \frac32\right)$, wherein the contour encloses $2$ poles, with the most common choice of $\log$
To resolve this issue, we simply choose $\log$ so that its branch cut doesn't intersect $\Gamma$, e.g., the one whose imaginary part takes values in $(-\epsilon, 2 \pi - \epsilon)$, where $\epsilon > 0$ is chosen small enough to avoid intersection, so that the Residue Theorem applies.
Illustration: A choice of branch cut for which the Residue Theorem can be applied
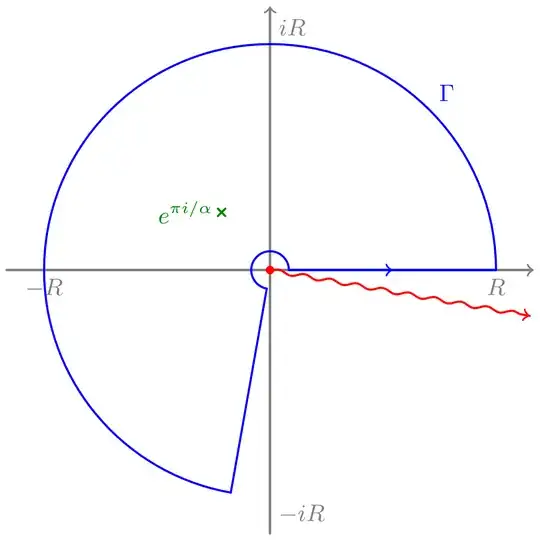
For such a choice of $\log$, $\Gamma$ encloses only a single pole, at $\exp \frac{\pi i}\alpha$, hence the Residue Theorem gives for all $\alpha > 1$ that
$$\oint_\Gamma \frac{dz}{z^\alpha + 1}
= 2 \pi i \operatorname{Res}\left(\frac{1}{z^\alpha + 1}; \exp \frac{\pi i}\alpha\right)
= -\frac{2 \pi i}\alpha \exp \frac{\pi i}{\alpha} ,$$
which leads to the usual formula,
$$\int_0^\infty \frac{dx}{x^\alpha + 1} = \frac\pi \alpha \csc \frac\pi\alpha .$$

