Solution of a transcendental equation

Question

Let $a_1,a_2,a_3,a_4,a_5 \in \mathbb{R}$, $a_1 \neq 0$ and consider the transcendental equation $$ (1) \quad a_1x^2 + a_2x + a_3 + a_4 e^{-2a_5x} + a_6 xe^{-a_5x} + a_7e^{-a_5x} = 0. $$ Is there a way to solve explicitly this equation? I know how to deal with it in the particular case with $a_1 = 1$ and $a_2 = a_3 = a_7 = 0$, that is, $$ x^2 + a_4 e^{-2a_5x} + a_6 xe^{-a_5x} = 0. $$ In this case, we multiply last equation by $e^{2a_5x}$ in order to obtain $$ e^{2a_5 x}x^2 + a_6xe^{a_5x} + a_4 = 0, $$ that is $$ (xe^{a_5x})^2 + a_6xe^{a_5x} + a_4 = 0 $$ and denoting $y = xe^{a_5 x}$ the equation becomes $$ y^2 + a_6y + a_4 = 0, $$ which has a solution and I know what to do. Is there a way to use this same idea to solve (1)?

Edit: Without loss of generality we can assume $a_1 = 1$.

Answer 1

Your method of resolution can be "reverse-engineered" as it follows. Substitute the variable $y = \alpha e^{-\lambda x} + \beta x + \gamma$ inside the quadratic equation $ay^2 + by + c = 0$ and compare the coefficients with your own parametrization, hence $$ \begin{cases} a_1 = a\beta^2 \\ a_2 = \beta(2a\gamma + b) \\ a_3 = a\gamma^2 + b\gamma + c \end{cases} \quad\&\quad \begin{cases} a_4 = a\alpha^2 \\ a_6 = 2a\alpha\beta \\ a_7 = \alpha(2a\gamma + b) \end{cases}, $$ letting aside the obviously renamed parameter $a_5 = \lambda$. In consequence, one understands that your method will be able to a solution to the original problem if and only if the above system of equations can be solved for $(a,b,c)$ and $(\alpha,\beta,\gamma)$ in terms of $a_{1,2,3,4,6,7,}$.

Unfortunately, not all cases can recasted as such, meaning that the present method fails to cope with every instances of the problem. Indeed, the reparametrization implies the subcondition $a^6 = (2\alpha\beta)^2 = 4a_1a_2$ for example, which is not fulfilled in general.

---

Addendum. In the cases where your change of variable works, then one needs to solve the following equation :
$$ \alpha e^{-\lambda x} + \beta x + \gamma = y_\pm, \;\;\text{with}\;\; y_\pm = \frac{-b\pm\sqrt{b^2-4ac}}{2a}. $$ Its solutions are given by $$ x_k^\pm = \frac{1}{\lambda}W_k\left(-\frac{\lambda\alpha}{\beta}e^{\lambda(\gamma-y_\pm)/\beta}\right) - \frac{\gamma-y_\pm}{\beta} $$ where $W_k$ is the $k^\mathrm{th}$ branch of the Lambert function.

Answer 2

1.)

$$a_1x^2+a_2x+a_3+a_4e^{-2a_5x}+a_6xe^{-a_5x}+a_7e^{-a_5x}=0$$ $$(a_1x^2+a_2x+a_3)+a_4e^{-2a_5x}+(a_6xe+a_7)e^{-a_5x}=0$$

You can solve the equation in terms of elementary functions if you set some of the $a_1,...,a_7$ to zero so that the equation contains either $x$ or $e^x$.

If the equation can be transformed to a polynomial equation with nonzero degree of both $x$ and $e^x$ simultaneously without a univariate factor, we don't know how to solve for $x$ by rearranging the equation by applying only finite numbers of only elementary functions.

If $a_1,...,a_7$ all are algebraic numbers and the equation can be transformed to a polynomial equation with nonzero degree of both $x$ and $e^x$ simultaneously without a univariate factor, the equation cannot have solutions that are elementary numbers except $0$.

Let $c$ be a constant. The equation is solvable in terms of elementary functions together with the nonelementary special function Lambert W

• if there is only one exponential monomial and one $x$-power monomial,
• if there is only one $e^{cx}$ and one summand linear in $x$,
• if there are only two exponential summands, or
• if there are only one or two exponential summands with factors linear in $x$.

Also, the equation can be simplified to some of these cases if all summands have a power of $x$ as factor.

2.)

Following your way:

$$a_1x^2+a_2x+a_3+a_4e^{-2a_5x}+a_6xe^{-a_5x}+a_7e^{-a_5x}=0$$

$$a_1x^2(e^{a_5x})^2+a_2x(e^{a_5x})^2+a_3(e^{a_5x})^2+a_4+a_6xe^{a_5x}+a_7e^{a_5x}=0$$

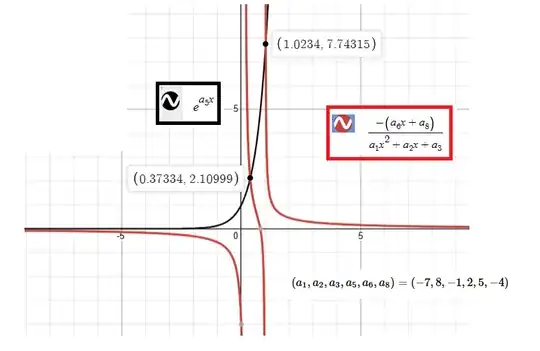
$$e^{a_5x}=\frac{1}{2}\frac{(-a_6x-a_7+\sqrt{a_6^2x^2+2a_6xa_7+a_7^2-4a_4a_1x^2-4a_4a_2x-4a_4a_3}}{a_1x^2+a_2x+a_3},-\frac{1}{2}\frac{a_6x+a_7+\sqrt{a_6^2x^2+2a_6xa_7+a_7^2-4a_4a_1x^2-4a_4a_2x-4a_4a_3}}{a_1x^2+a_2x+a_3}$$

This equation is solvable by Lambert W if the right-hand side of the equation is a linear term of $x$ or are a constant multiplied by $x^2$.

This equation is solvable by the Generalized Lambert W of Mező et. al. if the right-hand side of the equation is a rational expression of $x$.

We can build the corresponding equation systems and solve for $a_1,...,a_7$.

Answer 3

COMMENT.-With a plotter it is very easy. Without a plotter it is very difficult.

Example: We have $$e^{a_5x}=\frac{-(a_6x+a_8)}{a_1x^2+a_2x+a_3}\space \text {where } a_8=a_4+a_7$$