Prove or disprove that the envelope of some chords of a conic section is another conic section

Question

The problem is as follows:

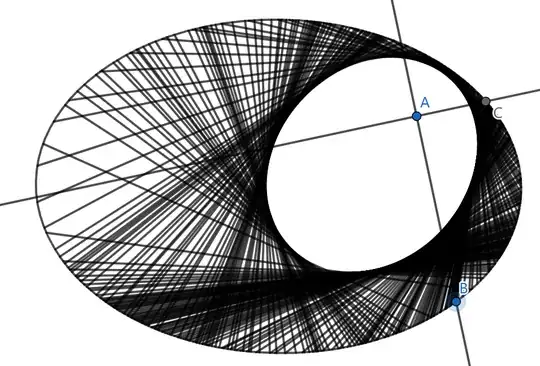
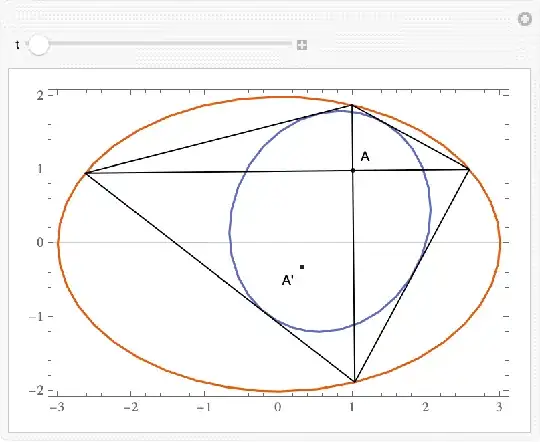
Let $\Gamma$ be an ellipse and $A$ is a point in the interior of $\Gamma$. Let $B,C$ be two moving points on $\Gamma$ such that $AB\perp AC$. Prove or disprove that the envelope of $BC$ is a conic section.

The picture is as follows

It seems that is the envelope is another ellipse, $A$ is one of the the Foci.

My attempt is like this. We know that for a tangent of $Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0$ on $(x_0,y_0)$ is

$$\begin{pmatrix} x_0 & y_0 & 1 \end{pmatrix}\begin{pmatrix} A & B & D\\ B & C & E\\ D & E & F \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}=0$$

So if the coefficient is $Ux+Vy+1=0$, then $(U,V)$ is on a conic section. Therefore, we set $\Gamma$ to be $ax^2+2bxy+cy^2+2dx+2ey+f=0$, $A(0,0)$, and set $B(x_1,y_1),C(x_2,y_2)$. The line is $x(y_1-y_2)+y(x_2-x_1)=x_1y_2-x_2y_1$ So we need to find some constant $a',b',c',d',e',f'$ (which only depends on $A,B,C,D,E,F$) which always

$$a'(x_1-x_2)^2+2b'(x_2-x_1)(y_1-y_2)+c'(y_1-y_2)^2+2d'(x_1-x_2)(x_1y_2-x_2y_1)+2e'(y_1-y_2)(x_1y_2-x_2y_1)+f'(x_1y_2-x_2y_1)^2=0$$

With constraints $ax_1^2+2bx_1y_1+cy_1^2+2dx_1+2ey_1+f=0$, $ax_2^2+2bx_2y_2+cy_2^2+2dx_2+2ey_2+f=0$, and $x_1x_2+y_1y_2=0$.

But I am unable to find it, since the $y_1^2y_2^2$ terms in $(x_1y_2-x_2y_1)^2$ (using $x_1x_2+y_1y_2=0$) is tough to think... May I ask is there any ideas...?

Answer 1

Let $f(x,y) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 = 0$ be the equation of the original ellipse. Let $P=(u,v)$ be a point in the ellipse other than $A = (x_0,y_0)$ and let $\ell$ be a line through $P$, say $y-v = m(x-u)$, where $m$ is a free parameter (the slope). It intersects the ellipse at two points $Q=(x_1,y_1)$ and $R=(x_2,y_2)$, where $x_{1,2}$ are the two real solutions to the quadratic equation $$ f(x,m(x-u)+v) = \left(\frac{1}{a^2} + \frac{m^2}{b^2} \right)x^2 + \frac{2m(v-mu)}{b^2}x + \frac{(v-mu)^2}{b^2} - 1 = 0. $$ The angle $\theta$ subtended by the chord $QR$ at $A$ is given by $$ \cos \theta = \frac{QA^2 + RA^2 - QR^2}{2 QA \cdot RA}. $$

The hole (i.e., the region not covered by the line segment $BC$) is precisely the set of all $P$ for which $\theta$ is larger than $\pi/2$ for all $m$.

In other words, for all $m$, we want $$ \cos \theta < 0 \implies QA^2 + RA^2 < QR^2. $$ Expanding each side gives $$ QR^2 = (x_1-x_2)^2 + (y_1-y_2)^2= (m^2+1) [(x_1+x_2)^2 - 4x_1 x_2], $$ and \begin{align} QA^2 + RA^2 &= (x_1-x_0)^2 + (y_1-y_0)^2 + (x_2-x_0)^2 + (y_2-y_0)^2 \\ &= (x_1+x_2)^2 - 2x_1x_2 - 2x_0(x_1+x_2) + 2x_0^2 \\ &\qquad + (y_1 + y_2)^2 -2y_1y_2 -2y_0(y_1+y_2) + 2y_0^2 \\ &= (m^2+1) [(x_1+x_2)^2 - 2x_1x_2] - 2[x_0 + m(y_0 - v+mu)](x_1+x_2) \\ &\qquad + 2[(y_0-v+mu)^2 + x_0^2]. \end{align} Therefore, using Mathematica for the cumbersome calculation, we have \begin{align} &QR^2 - (QA^2 + RA^2) \\ &= -2(m^2+1)x_1x_2 - 2[x_0 + m(y_0 - v+mu)](x_1+x_2) \\ &\qquad + 2[(y_0-v+mu)^2 + x_0^2] \\ &= \frac{1}{b^2+a^2m^2} \Big[ \left(2 a^2 [b^2-(u-x_0)^2-y_0^2]-2 b^2 u^2\right)m^2 \\ &\qquad + 4 \left[a^2 v (u-x_0)+b^2 u (v-y_0)\right]m + 2 a^2 (b^2-v^2) - 2b^2 [(v-y_0)^2+x_0^2] \Big]. \end{align} where we substituted $x_1+x_2$ and $x_1x_2$ from the quadratic equation above using Vieta's formulas. We want this quantity to be positive for all $m$, which means the discriminant of the quadratic inside brackets must be nonpositive. Using Mathematica again yields \begin{align} & 16 b^2 \left[(a^2 + b^2) (a^2 - x_0^2) - a^2 y_0^2\right] u^2 -32 a^2 b^2 x_0 y_0 \, u v + 16 a^2 \left[(a^2 + b^2)(b^2 - y_0^2) - b^2 x_0^2 \right] v^2 \\ &32 a^2 b^2 x_0 (x_0^2 + y_0^2 -a^2)\,u + 32 a^2 b^2 y_0 (x_0^2 + y_0^2-b^2)\, v - 16 a^2 b^2 (x_0^2 + y_0^2-a^2) (x_0^2 + y_0^2-b^2) \le 0. \end{align} While the expression looks quite cumbersome, the interesting thing to note is that it is quadratic in $u$ and $v$. Therefore, the boundary of this region is a conic section, answering the question in the positive.

Let us verify that it's an ellipse by computing its discriminant using Mathematica again. Indeed, $$ -1024 a^2 b^2 (a^2 + b^2) (a^2 + b^2 - x_0^2 - y_0^2) (a^2 b^2 - a^2 y_0^2 - b^2 x_0^2)<0, $$ which follows from $$ a^2 > x_0^2,\qquad b^2 > y_0^2,\qquad a^2 b^2 - a^2 y_0^2 - b^2 x_0^2 = -a^2b^2 f(x_0,y_0) > 0, $$ because $A$ is inside the original ellipse. Moreover, the foci can be computed using the approach given in this answer. They are $$ A = (x_0,y_0),\qquad A' = \frac{a^2-b^2}{a^2+b^2}(x_0,-y_0). $$ One can also compute the eccentricity of this ellipse using this expression from Wikipedia: $$ e = \sqrt{\frac{b^4 x_0^2 + a^4 y_0^2}{a^2 b^2 (a^2 + b^2 - x_0^2 - y_0^2)}} < 1, $$ where the inequality follows from $$ [a^2 b^2 (a^2 + b^2 - x_0^2 - y_0^2)] - (b^4 x_0^2 + a^4 y_0^2) = -a^2 b^2 (a^2+b^2) f(x_0,y_0) > 0. $$

Here's an example illustrating all the interesting objects.