Why do powers of $\operatorname{sinc}$ converge to a Gaussian function?

Question

I am looking to find an intuition for how powers of the $\text{sinc}$ function behave. Just for context, the $\text{sinc}$ function I'm looking at is the "unnormalized" one:

$$ \text{sinc}(x) = \begin{cases} 1 &\text{if}\, x = 0\\ \frac {\sin x} {x} &\text{otherwise.} \end{cases} $$

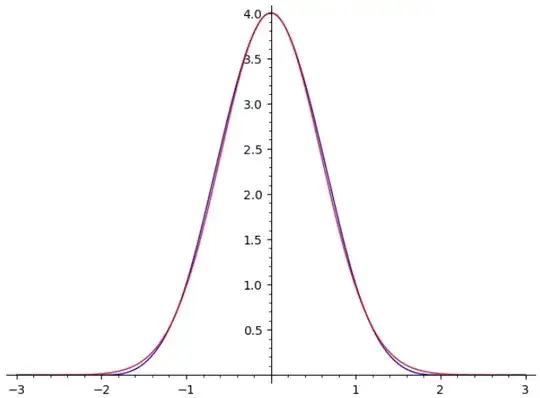
Consider this sequence of functions:

$$ f_n(x):= \text{sinc} \left( \sqrt{\dfrac{3}{n}} \cdot x \right) ^ {n} $$

where $n \in \mathbb{Z}$. As $n \to \infty$, my conjecture is that $f_n \to g$ uniformly, where $g$ is a Gaussian function:

$$ g(x) := \exp {\left( -x^2 / 2 \right)} $$

Expanding the Taylor series of $f_n$ and $g$ around $x = 0$, I obtain:

$$ f_n(x) = 1 - \frac{1}{2} x^2 + \left( \frac{1}{8} - \frac{1}{20n} \right) x^4 - \left( \frac{1}{48} - \frac{1}{40n} + \frac{1}{105n^2} \right) x^6 + \left( \frac{1}{384} - \frac{1}{160n} + \frac{101}{16800n^2} - \frac{3}{1400n^3} \right) x^8 + O(x^{10}) \\ g(x) = \sum_{k=0}^{\infty}{\dfrac{(-1)^k x^{2k}}{2^k k!}} = 1 - \frac{1}{2} x^2 + \frac{1}{8} x^4 - \frac{1}{48} x^6 + \frac{1}{384} x^8 + O(x^{10}) \\ $$

(I expanded the series for $f_n$ by way of reference to this question & using Wolfram Alpha.)

I can see that the terms with $n$ in the denominator in the series coefficients for $f_n$ will vanish as $n \to \infty$, leaving only the leading term. Inspecting the first dozen or so of those leading terms confirms they equal the coefficients in the series for $g$, reinforcing my suspicion that $f_n \to g$ uniformly.

But simply comparing the "first few" coefficients by inspection leaves me feeling... unenlightened. Is there an elegant way to prove that $f_n \to g$ uniformly? Would it be sufficient to prove that the non-vanishing terms in the coefficients of the series expansion for $f_n$ will continue to equal $\frac{(-1)^k}{2^k k!}$ out to $k=\infty$? And if so, how does one approach that proof?

(And, by the way: is there any particular underlying intuition for why the argument of $\text{sinc}$ must be scaled by a factor of $\sqrt{3}$?)

More broadly: are there some more general mathematical concepts I can leverage to better understand what's going on? Looking at the generality of results like the central limit theorem, as well as questions like this - is it just incidental that $\text{sinc}$ was the function I happened to be messing around with this one particular lazy Sunday, and actually this type of convergence to a Gaussian happens for a much wider class of sequences of functions? My interest here is purely recreational (and this isn't "for" anything in particular)... so more abstract answers / hand-wavey "proofs" / generalized discussion / nudges in the right direction for me to run with the rest of the way are all very welcome. ;)

Thank you!

Answer 1

Your issue is explainable in a clean way with Fourier transform and spline functions.

Let us denote by $\chi$ the characteristic function $\chi_{[-\tfrac12,\tfrac12]}$ of interval $[-\tfrac12,\tfrac12]$ (also called "rectangular function", especially in Signal Processing).

Fourier transform

• maps $\operatorname{sinc}(x)$ onto $\chi(u)$ (reference here) for a certain normalization of Fourier Transform).

Therefore :

• maps $\operatorname{sinc}^n(x)$ (ordinary power) onto $s_n(u):=\chi^{*n}(u)$ (convolution power), which happens to be a special kind of spline function.

It is known that $s_n$ (conveniently rescaled) converges to a gaussian curve, when $n \to \infty$ (see how this convergence is quick on Fig. 1 below for $n=4$).

As the Inverse Fourier Transform of a gaussian function is a gaussian function, coming back in the original space of variable $x$, we have established the result : we have indeed a gaussian function.

Besides, there is a handy explicit formula expressing $s_n:=\chi^{*n}$ given here expressing it as a spline function (with a shift because in the reference just given, interval $[0,1]$ is used instead of interval $[-\tfrac12,\tfrac12]$).

For example, for $n=4$ we have:

$$s_4(x)=\chi^{*4}(x)=(x+2)_+^3-4(x+1)_+^3+6(x)_+^3-4(x-1)_+^3+(x-2)_+^3$$

(please note alternate sign binomial coefficients)

where $x_+:=\max(0,x)$ (called "ramp function" in Signal Processing).

See for example the representative curve of $\chi^{*4}$ (Fig. below) obtained with the following Sage program :

 r(x)=max_symbolic(0,x)^3
 f(x)=r(x+2)-4*r(x+1)+6*r(x)-4*r(x-1)+r(x-2)
 g=plot(f(x),(x,-3,3))
 g+=plot(4*exp(-x^2/0.7071),(x,-3,3),color='red')
 show(g)

Fig. 1 : The (blue) spline curve of $s_4$, and its excellent approximation by a (red) gaussian curve (see program).

Remark : The blue curve above is in fact polynomial by intervals with at most third degree expressions on each interval $[k,k+1]$, $k=-2,-1,0,1$ of so-called Bezier curves.

Important remark : Almost all this can be explained in a probabilistic framework : $\chi^{*n}$ can be interpreted as the pdf of the sum $S_n$ of $n$ uniformly distributed independent random variables on $[-\tfrac12,\tfrac12]$, and it is known (Central Limit Theorem, that you have mentionned in your question) that $\tfrac{1}{n}S_n$ converges (in law) to the standard gaussian distribution $N(0,1)$. (please note that multiplication by $\tfrac{1}{n}$ is equivalent to a normalization).