I was playing around with continued fractions, and while trying to find an explanation for a different occurrence than I am going to talk about here, I was able to make a summation equivalent to the continued fraction of ax: meaning for some number a, as the value of u goes to infinity for this summation, the result approaches
$$ a+\cfrac{1}{2a+\cfrac{1}{3a+\cfrac{1}{4a+\cdots}}} $$
$(a * 1 + 1/(a * 2 + 1/(a * 3 +...)$
For the case where $a = 1$, this approaches the continued fraction constant. I do not know of any closed-form version of this number, although there might be one that I just haven't seen, but I was wondering if this summation could be evaluated to possibly find one. Also, I am sorry if I am not explaining this well and for not using the stack exchange code, I am new to stack exchange and haven't figured out how to use it yet. Here is a screenshot of the summations that I am talking about in Desmos.
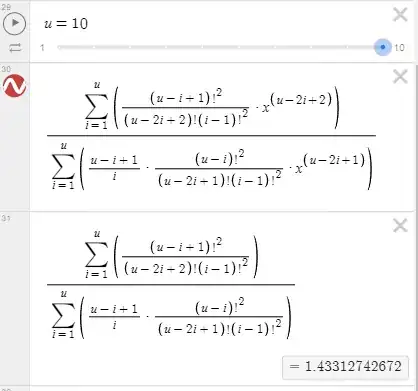
\cfracfunction. – Jean Marie Nov 24 '24 at 10:15