3

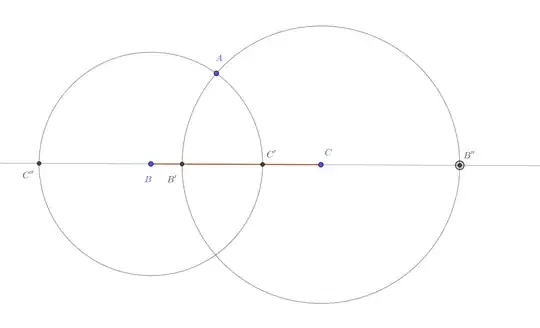
Standard high school geometry courses cover the Triangle Inequality, which states that if $a,b,c$ are three sides of a triangle, then $$a + b > c \qquad a + c > b \qquad b + c > a$$ I'm interested in the converse:

If $a,b,c$ are three positive real numbers satisfying the above three constraints, does there exist a triangle with those three lengths as the side lengths?

I'm not sure how to tackle a question like this in the axiomatic system used in a high school geometry course. If we use a coordinate system, then it should be easy to specify the vertices of the appropriate triangle, but what if we stick fully within the confines of classical geometry, where points are not given coordinates?

Blue
  • 83,939
Nick A.
  • 2,333

2 Answers2

2

We can and do assume that $a$ is the biggest side. We draw a segment $BC$ of length $a$. Consider now a circle with radius $c$ centered in $B$, and a circle with radius $b$ centered in $C$. By the maximality assumption, these circles intersect each the segment $BC$ in exactly one point, so we obtain two points on $BC$ denoted by $C',B'$ so that $BC'=c$, $CB'=b$. If we intersect the two circles with the line $BC$, then each circle gets one more intersection point, denote them by $B'', C''$:

mathematics stack exchange 5000827 :: picture

Because $b+c>0$ the points introduced so far are on the line $BC$ in the following order: $C'',B,B';C',C,B''$.

Now we can argue by continuity, or explicitly find the projection of $A$ on $BC$ using a suitable coordinate system. I find the continuity argument simpler. The arc from $C'$ to $C''$ of the circle centered in $B$ in the upper half-plane (chose one if there is no upper) starts (in $C'$,) in the interior of the circle $\odot(C)$ centered in $C$, and ends in the exterior of this circle. The plane is connected, so it intersects this circle $\odot(C)$. Denote this point by $A$. Then $\Delta ABC$ is one suitable triangle with sides $a,b,c$.

dan_fulea
  • 37,952
  • I like this method, but I wonder how we can argue by continuity while still staying within classical geometry. Is there a way we can endow the plane with a topology (so that continuity can be discussed) without resorting to just calling the plane $\mathbb{R}^2$? – Nick A. Nov 20 '24 at 19:04
  • @NickA. For those continuity concepts, check the references given in comments to my answer (which by now is basically identical to this one). You will not get by without some notion of continuity because otherwise this is just not true. – Torsten Schoeneberg Nov 24 '24 at 20:15
  • 1
    @TorstenSchoeneberg Oh, thanks for the comment, i see only now the previous one. School geometry is at some points very intuitive. I learned about the missing points in the after-school, there are finite geometries that still work. Here we need an order, too, so a field $F$ like $\Bbb Q$ or some upper field may be a good candidate to have a difference. In the affine space over $F$ we can define lines, equations are $sX+tY=u$, $s,t,u\in\Bbb F$. Lengths of triangle may live outside $F$, but inequalities make sense. In such a world two circles may not intersect over $F$, but do so over $\Bbb R$. – dan_fulea Nov 24 '24 at 20:33
1

I'd draw a line of length $c$ with endpoints $A$ and $B$, put a circle of radius $b$ around $A$ and a circle of radius $a$ around $B$. Once you show those two circles intersect at a point $C$ not on the original line, you have a triangle.

To show such an intersection point exists, imagine the points $A$ and $B$ on a straight line, with $A$ on the left, $B$ on the right. All points considered in the following lie on that straight line. We note that because of $b+c > a$, the leftmost point of the circle around $A$ is left of the leftmost most point of the circle around $B$; and because $a+b >c$, the rightmost point of the circle around $A$ is right of the leftmost point of the circle around $B$; but finally because $a+c > b$, that rightmost point of the circle around $A$ is still left of the rightmost point of the circle around $B$. That is, the circle around $A$ contains both a point inside and a point outside the other circle. Now one uses "circle-circle continuity" (see comments) to conclude.

Torsten Schoeneberg
  • 29,325
  • However, from a truly classical point of view, the fact that these circles have nontrivial intersection was something that Euclid assumed (in the middle of his construction of a perpendicular bisector) without stating any axioms to support it. – Lee Mosher Nov 19 '24 at 22:34
  • @LeeMosher: This is a well-known gap in "Elements", fixing the issue requires an extra axiom ("Circular continuity principle"). This is discussed in Greenberg's book, page 94. – Moishe Kohan Nov 19 '24 at 23:04
  • Thanks for both comments! An on-site reference for a discussion of "circle-circle continuity" is https://math.stackexchange.com/q/2074781/96384. – Torsten Schoeneberg Nov 20 '24 at 21:35