can you please help me with this problem? I have thought that in order to be solved, you need $\gcd(21, 6a-1)=1$ as a condition. That means that $6a-1$ is not $\equiv 0 \bmod 7$ and $\bmod 3$. While the first condition means that a cannot be congruent to $6$, so it can be one of the elements of $\{1,2,3,4,5\}$, the second one is valid for each value of a $\{1,2\}$. the intersection of this set is $\{1,2\}$ and the system is valid only if $a \equiv 2 \bmod 7$ but since $a \equiv 2 \bmod 3 \implies a \equiv 4 \bmod 7$. Is this method correct? Sorry for the English but I am not mother tongue.
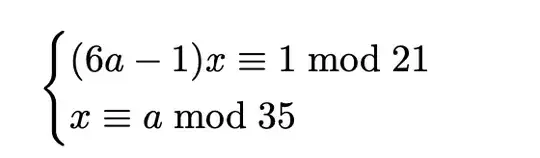
Asked
Active
Viewed 30 times
0
Bill Dubuque
- 282,220
Irene
- 19
-
Please use MathJax. Here is a tutorial. Do you mean $\gcd(21,6a-1)=1$ as condition? – Dietrich Burde Nov 17 '24 at 16:39
-
yes, I mean that, I wrote the italiano version. My bad – Irene Nov 17 '24 at 16:42
-
No problem. If you use MathJax, the language is not an issue. The command is "\gcd". Images are not good, see here, why. – Dietrich Burde Nov 17 '24 at 16:48
-
$(6a-1,21)$ is indeed necessary. Next apply the linked fractional CRT solvability criterion to deduce it is solvable $\iff !\bmod 7!:\ (6a-1)a\equiv 1\cdot 1\iff 0\equiv a^2+a+1\equiv (a-2)(a+3)\ \ $ – Bill Dubuque Nov 17 '24 at 19:10
-
Okay I did it! But to find the general solution, what value of a should I use? – Irene Nov 17 '24 at 20:06