3

The vertices of a cross-polytope can be chosen as the unit vectors pointing along each co-ordinate axis – i.e. all the permutations of $(±1, 0, 0,\dots, 0)$. The cross-polytope is the convex hull of its vertices.

Consider the section of a cross-polytope $β_n$ with vertices $(±1, 0, 0,\dots, 0)\in\mathbb{R}^n$ by the hyperplane $(1,1,\dots,1)\cdot\mathbf x=d$.
Its total edge length is constant for all $|d|<1$.

I verified it for $n=2,3,4$. I wonder if this is still true for higher dimensions.

For $n=2$, cross-polytope $β_2$ is a square of side length $\sqrt2$. The line $(1,1)\cdot\mathbf{x}=d$ cuts $β_2$ along a segment of constant length $\sqrt2$ for all $|d|<1$.

For $n=3$, cross-polytope $β_3$ is a regular octahedron of edge length $\sqrt2$. The plane $(1,1,1)\cdot\mathbf{x}=d$ cuts $β_3$ along a hexagon the length of whose perimeter is constant $3\sqrt2$ for all $|d|<1$.

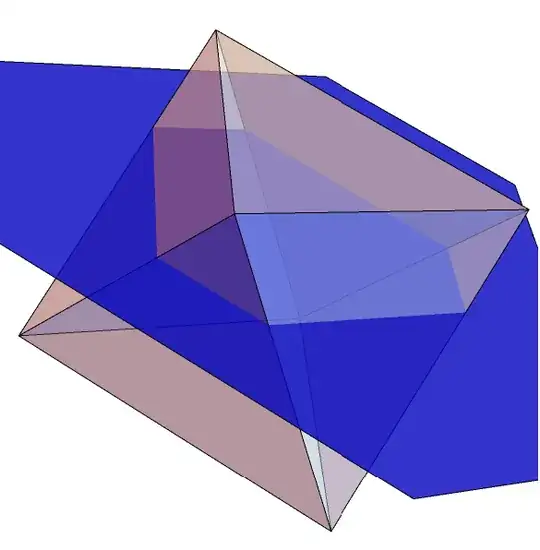
For $n=4$, cross-polytope $β_4$ is a 16-cell of edge length $\sqrt2$. The hyperplane $(1,1,1,1)\cdot\mathbf x=d$ cuts $β_4$ along a solid with 8 triangle faces and 6 rectangle faces. Its total edge length is constant $12\sqrt2$ for all $|d|<1$.

hbghlyj
  • 5,361
  • 1
    Nice question. I'm sure it's true. If true then the total edge length is the total edge length of the simplex with side $\sqrt{2}$ (the zeroth slice), which is $n(n-1)\sqrt{2}/2$ so check your calculation for $n=4$. – Ethan Bolker Nov 12 '24 at 21:52
  • I think that at $d=1$ you always have the simplex with the standard basis vectors as vertices. All the "other edges" you see when $d < 1$ have shrunk to $0$. – Ethan Bolker Nov 12 '24 at 22:14
  • When $n=4$ The $d=1$ slice is the convex hull of $(1,0,0,0), (0,1,0,0),(0,0,1,0),(0,0,0,1)$ . That's a regular tetrahedron. – Ethan Bolker Nov 12 '24 at 22:21
  • I think that when $n=4$, the total edge length at $|d|<1$ is twice the total edge length at $d=1$. From the GIF, two edges seem to coincide into one edge when $|d|$ goes to 1. – hbghlyj Nov 12 '24 at 22:26
  • You're right, and so is @Dr.RichardKlitzing ;s answer. – Ethan Bolker Nov 12 '24 at 22:28

1 Answers1

2

Let x3o3o..o3o4o ($n$ nodes) be the $n$-D Coxeter-Dynkin diagram of the according regular cross-polytope or orthoplex. Then clearly x3o3o...o3o . ($n-1$ nodes) is the $(n-1)$-D Coxeter-Dynkin diagram of its (all equivalent) facets, then each being according regular simplices.

Note further that the opposite facet here generally happens to be a dually arranged simplex. As a Coxeter-Dynkin diagram this is just o3o3o...o3x (again $n-1$ nodes).

Further those two opposite facets (as bases) are connected by further simplexes (as sides), thus generalising the structure of an antiprism.

Esp. the facet parallel cross-section of the orthoplex then is given by y3o3o...o3z (still $n-1$ nodes), where those two edge sizes are related to the former by $z=x-y$.

And these extremally expanded simplexes x3o3o...o3x ($n-1$ nodes) generally do have $n!/(n-3)!$ edges, i.e. the here half-symmetric variant y3o3o...o3z would have $\frac12 n!/(n-3)!$ edges of size $y$ plus $\frac12 n!/(n-3)!$ edges of size $z=x-y$. This in turn makes clear that the total sum of edge length (in units of length $x$) is just $\frac12 n!/(n-3)!$, independent of sectioning depth (as long as neither $y$ nor $z$ are degenerate).

In contrast, the edge count of the regular $(n-1)$-D simplex x3o3o...o3o, i.e. the facet of the orthoplex, clearly is $\frac12 n!/(n-2)!$.

--- rk

Dr. Richard Klitzing
  • 5,757