1. Some Familiar Facts about the Cubic Newton Fractal
The cubic Newton fractal is the Julia set, in the complex plane, for iterations of $z \mapsto z - (z^3 - 1) / (3 z^2)$; shown in
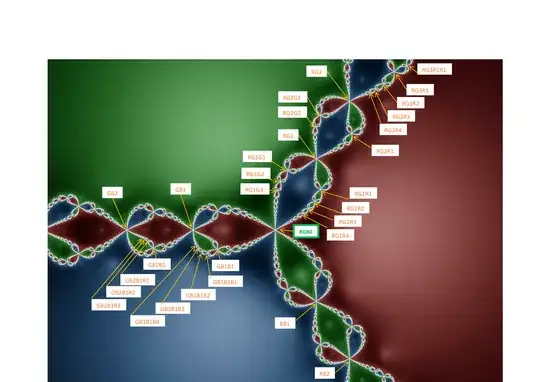
this picture as "necklace mesh" of white points, on the closed rectangle patch of (roughly) $z \in (2, 1.5) \times (-1.5~{\rm I}, 1.5~{\rm I})$.
The following notions correspond to certain features of the picture, and are relevant for my question below:
the Julia set, i.e. "the fractal" itself, depicted as "necklace pattern" of bright white colored points; constituting a connected fractal mesh of boundary lines between
three Fatou sets (depicted as all red points, all green points, and all blue points, resp.), each consisting of "infinitely many" disjoint
basins of attraction (in the following short "basins") of the corresponding color. As they appear in the picture above, some basins "run all the way" to the edge of the picture rectangle (this includes "the three big, principal basins" of the three Fatou sets, which together fill most of the picture area); while each more typical "small basin" appears completely enclosed by a white boundary line (i.e. a corresponding circular segment of the Julia set).
Especially relevant is the "(self-)similarity, over all length scales" of the cubic Newton fractal (incl. Julia set and the "arrangement of basins"); in some detail:
that each point of the Julia set is a common boundary point of exactly six basins; specifically of two of each of the three Fatou sets (and thus always shown as each white point as the common boundary point of corresponding specific two red, two blue, and two green basins), and
that "there is no extended stretch of boundary line" in common for any two basins; but instead:
any two basins share at most several disconnected boundary points (which in turn all belong to the Julia set, of course).
2. The "Shamrock Nodes" as conspicuous points of the Julia Set, and a scheme for systematically identifying, naming and enumerating Shamrock Nodes in sequence
By its particular symmetry and self-similarity, certain points of the cubic Newton fractal stand out more or less conspicuously -- for lack of other role models I'll call them "shamrock nodes" in the following.
Foremost the point $(0, 0)$, at the center of symmetry, i.e. the only point (shown in the picture) which the three big, principal basins of attraction have as their common boundary point. The three other, smaller basins of attraction which border on this point are readily recognized as part of a shamrock shape ("three-leaf clover shape") in the complex plane; with this most conspicuous "shamrock node" $(0, 0)$ at its center.
Naming this particular point $(0, 0)$ in this context suggestively point RGB$\mathbf{0}$, it can serve as initial point in successively identifying and naming (at least some countable set of) additional "shamrock nodes" of the cubic Newton fractal;
by the following algorithm: ... which could be arbitrarily verbose and lengthy to state explicitly ...
So: perhaps the following sketch is at least as instructive, but easier to digest:
Since above I claimed that a countable sequence (enumeration) of "shamrock nodes" can be obtained, I'll still put some concrete example of the initial sequence in the following "Spoiler":
RGB$\mathbf{0}$, RG1, RG2, RB1, RG1R1, RG3, RB2, GB1, RG1R2, RG1G1, RB1R1, RB1B1, GB1G1, GB1B1, RG4, RB3, GB2, RG1R3, RG1G2, RB1R2, RB1B2, GB1G2, GB1B2, RG2R1, RG1R1R1, RG5, RB4, GB3, RG1R4, RG1G3, RB1R3, RB1B3, GB1G3, GB1B3, RG2R2, RB2R1, RB2B1, GB2G1, GB2B1, RG1R1R2, RG3R1, RG1R1G1, RG1G1R1, RG1G1G1, RB1R1R1, RB1R1B1, RB1B1R1, RB1B1B1, GB1G1G1, GB1G1B1, GB1B1G1, GB1B1B1, RG6, RB5, GB4, ...
3. My question is about: Placing an "Open Disk" on each Shamrock Node
Considering an (uncountable) set of points (such as the Cubic Newton Fractal - "white necklace" Julia Set) and a (countable) subset (such as the sequence of Shamrock Nodes), all given as points of a complete metric space, in the present case specifically with $\rm d[ ~ p, q ~] := | ~ z[ ~ q ~ ] - z[ ~ p ~ ] ~|$,
it is a rather common technique and persuit in topology to define certain sequences of (generally open) subsets of the bigger (uncountable) set in terms of the points of the smaller (countable) subset,
and to investigate whether, or not, the bigger (uncountable) set is covered by the defined open sets;
all of them, constituting "a family" of open sets, "taken" together (as union of those sets).
Concrete examples of such question and answers can be found here and the "related questions" listed there.
Hereby I'd like to ask such a type of question, as simple and straightforward as reasonable, about the Cubic Newton Fractal (Julia Set) and its Sequence of Shamrock Nodes defined (or presently at least sketched) above:
4. My question:
Considering a family $\mathcal F$ of open disks in the complex plane, where each point in the infinite list $\mathfrak S_{\text{CNF}}$ of "shamrock nodes" of the cubic Newton fractal (Julia set) is the center of an open disk (each of non-zero radius, without further requirements), i.e.
$$\mathcal F := \{ ~ D_k \subset \mathbb C ~ | ~ (\mathfrak s_k \in \mathfrak S_{\text{CNF}}) \text{ and } (\exists ~ r_k > 0 : \forall ~ z \in \mathbb C : (z \in D_k) \iff (| ~ z - \mathfrak s_k | < r_k)) ~ \},$$
is family $\mathcal F$ guaranteed an open cover of the cubic Newton fractal (Julia set) ?
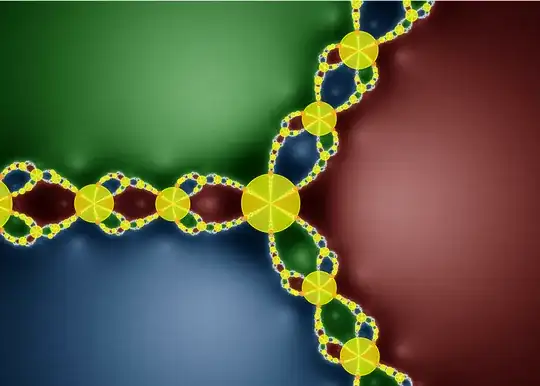
5. Appendix: An illustration ("Artist's Impression") of some open disks having been placed on part of the initial sequence of Shamrock Nodes
(Note however: The choice of disk radii in this picture is not completely arbitrary, aside from being finite at all, as my question is asking; but instead rather "deliberately artistic".)