$f:\mathbb{R} \setminus \{1\} \to \{(x,y) \in \mathbb{R}^2 : y^2=x^2(1+x)\}$, $f(t)=(t^2-1,t(t^2-1))$ is a local homeomorphism

Question

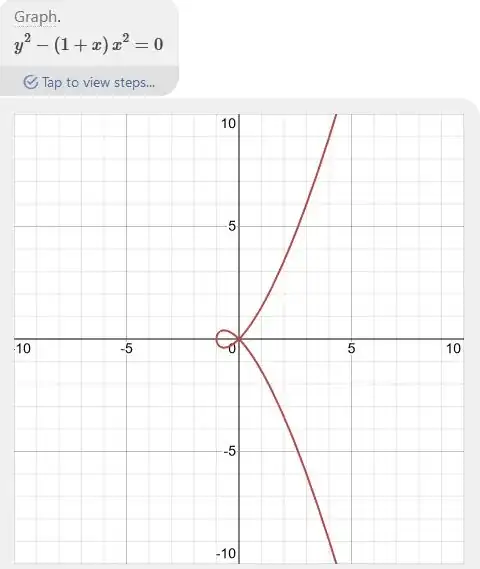
Let be $\,\,f:\mathbb{R} \setminus \{1\} \to \{(x,y) \in \mathbb{R}^2 : y^2=x^2(1+x)\} \,\,$ with $\,\,\,f(t)=(t^2-1,t(t^2-1))$, prove that for all $x \in \mathbb{R}\setminus \{1\}$ exists a neighborhood $U$ of $x$ such that $f:U \to f(U)$ is a homeomorphism.

Now $f$ is continuous and bijective and I want to show that if $t \in \mathbb{R} \setminus \{1\}$ exists a $\delta>0$, if necessary we can take $\delta$ so that $t-\delta>1\,\,\,$ or\and $\,\,t+\delta<1\,\,\,$, such that $\,\,\,f: (t- \delta, t+ \delta) \to f((t- \delta, t+ \delta))\,\,\,$ is a open map, that is for all $u \in (t- \delta, t+ \delta)\,\,$ exists a $\,\,\,\epsilon >0\,\,\,\,$ such that $\,\,\,\,B_{\mathbb{R}^2}(f(u),\epsilon)\,\,\cap\,\, \{y^2=x^2(1+x)\} \subseteq f((t- \delta, t+ \delta))$.

I think that $\epsilon < \mathrm{min} \, \{|t-u|,|t+u|\}$ could work, any hint to show it properly? If I am not wrong.

Answer 1

All you have to know is that $f$ is continuous and injective.

Given $t \in \mathbb R \setminus \{1\}$, take any closed interval $[a,b] \subset \mathbb R \setminus \{1\}$ such that $t \in (a,b)$. Then $f$ restricts to a continuous bijection $f_{[a,b]} : [a,b] \to f([a,b])$. Since $[a,b]$ is compact and $f([a,b])$ is Hausdorff, $f_{[a,b]}$ is a homeomorphism. Therefore the restriction $f_{(a,b)} : (a,b) \to f((a,b))$ of $f_{[a,b]}$ is also a homeomorphism.

Remark 1. We can generalize this as follows.

Let $f : X \to Y$ be a continuous injection between topological spaces. If each $x \in X$ has a compact neighborhood and $Y$ is Hausdorff, then for all $x \in X$ there exists an open neighborhood $U$ of $x$ such that $f :U \to f(U)$ is a homeomorphism.

Note that the condition on $X$ is a variant of local compactness. See Example of compact whose open subspace is not locally compact.

Remark 2. Usually a local homeomorphism $f : X \to Y$ is defined as continuous map such that each $x \in X$ has an open neighborhood $U$ which is mapped by $f$ homeomorphically onto an open subset of $Y$. For later use we observe that this implies that each open neighborhood $U'$ of $x$ which is contained in $U$ is mapped by $f$ homeomorphically onto an open subset of $Y$.
See When is a local homeomorphism a covering projection? and Wikipedia.

In this sense your map $f$ is no local homeomorphism. Look at the codomain $Y \subset \mathbb R^2$ of $f$:

It is fairly easy to see that $f$ maps

• $(1,\infty)$ homeomorphically onto the intersection of $Y$ with the open first quadrant
• $(-1,1)$ homeomorphically onto the intersection of $Y$ with the open laft halfplane
• $(-\infty,-1)$ homeomorphically onto the intersection of $Y$ with the open fourth quadrant

The problematic point is $t = -1$. Each open $V \subset Y$ with $f(-1) = (0,0) \in V$ contains points in the open first quadrant. However, no open neighborhood $U$ of $-1$ which is contained in $(-\infty,1) \subset \mathbb R \setminus \{1\}$ can map onto such $V$ because $f((-\infty,1))$ does not contain any point in the open first quadrant Now recall the above "For later use".