Solving integral $\int_{-\infty}^{\infty} \frac{k^2}{(4k^2+a^2\pi^2)\sinh^2(k)}dk $

Question

I stumbled across this integral:

$$I(a) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x)T(x-x', a)f(x') dx dx'$$ with: $$f(x)=1/\cosh(x)^2 \text{ and } T(x, a)=e^{-|a||x|}$$

I think it's easier to solve using the Fourier Fransform of these functions because we find:

$$I(a)= \int_{-\infty}^{\infty} |\hat f(k)|\hat T(k, a)dk $$

Which ends up being: $$ I(a)=8a\int_{-\infty}^{\infty} \frac{K^2}{(4K^2+a^2\pi^2)\sinh^2(K)}dK $$

Which I think is simpler to deal with. In the limit $a=0$, the real space integral gives $I(0)=4$, however I have no idea how to do something when $a\neq0$. I guessed that residues might be a good idea but $\sinh^2(x)$ contains an infinite number of them which seem painful to deal with.

Any idea is appreciated! Even in the form of a series in $a$!

Edit

I tried using the residues. I'll denote the integrand $f(K, a)$

The residues arising from $1/\sinh(K)$ in the complex planes are in $K = i\pi n$ with $n$ positive integers and are: $$res(f, n)=16in\dfrac{a^3}{(a^2-4n^2)^2\pi}$$

From Mathematica, I obtain:

$$\sum_{n>1}res(f, n)=\dfrac{ia^2}{2\pi}\left(\Psi_1(1-a/2)-\Psi_1(1+a/2)\right)$$

With $\Psi$ the first Polygamma function.

The residue in the upper half of the complex plane arising from the term in $1/(4K^2+a^2\pi^2)$ is $-ia^2\pi/(\sinh(a\pi/2)^2/2)$.

Unfortunately, I don't obtain the same thing with the residues (orange) and by direct numerical integration of $I$ (blue):

Probably because we have poles at $\infty$ and Jordan's lemma cannot apply?

Answer 1

Probably, regularization is a shortcut to the answer. We consider $(b>0)$ $$I(a,b)=8a\int_{-\infty}^\infty\frac{x^2}{(4x^2+\pi^2a^2)(\sinh^2x+b)}dx$$ $$=2a\int_{-\infty}^\infty\frac{dx}{\sinh^2x+b}-2a\left(\frac{\pi a}2\right)^2\int_{-\infty}^\infty\frac1{x^2+\big(\frac{\pi a}2\big)^2}\,\frac1{\sinh^2x+b}dx=I_1+I_2$$ where we can treat every integral separately. $$I_1=4a\int_{-\infty}^\infty\frac{dx}{\cosh(2x)+b-1}\overset{e^{2x}=t}{=}4a\int_0^\infty\frac{dt}{t^2-2t(1-b)+1}$$ $$=\frac{4a}{\sqrt{1-(1-b)^2}}\left(\pi-\arctan\frac{\sqrt{1-(1-b)^2}}{1-b}\right)\tag{1}$$ $$I_1(b\to0)=\frac{4\pi a}{\sqrt{2b}}-4a+O(\sqrt b)\tag{1a}$$ $$I_2=-8a\left(\frac{\pi a}2\right)^2\int_{-\infty}^\infty\frac1{x^2+(\pi a)^2}\,\frac1{\cosh x-1+b}dx$$ $$=-2a^2\pi\,\Re\int_{-\infty}^\infty\frac1{\frac a2-it}\,\frac1{\cosh 2\pi t-1+b}dt$$ $$=-4\pi a^2\Re\frac{\partial}{\partial a}\int_{-\infty}^\infty\frac{\ln(\frac a2-it)}{\cosh2\pi t-1+b}dt$$ Using the fact that $\ln\Gamma\big(\frac a2-i(z+i)\big)-\ln\Gamma\big(\frac a2-iz\big)=\ln\big(\frac a2-iz\big)$ and that $\cosh(2\pi (z+i))=\cosh(2\pi z)$, we can present $I_2$ as a contour integral along the rectangular contour $C:\,\,-R\to R\to R+i\to -R+i\to-R;\,R\to\infty$ $$I_2=4\pi a^2 \Re\frac{\partial}{\partial a}\oint_C\frac{\ln\Gamma\big(\frac a2-iz\big)}{\cosh2\pi z-1+b}dz=4\pi^2a^2\Re\sum\operatorname{Res}\frac{\psi\big(\frac a2-iz\big)}{\cosh2\pi z-1+b}$$ Denoting $1-b=\cos 2\pi s$, we have two simple poles inside the contour: at $z=is$ and $z=i(1-s)$.

The residue evaluation is straightforward and gives $$I_2=4\pi^2a^2\Re\, i\left(\frac{\psi\big(\frac a2+s\big)}{2\pi i\sin2\pi s}+\frac{\psi\big(\frac a2+1-s\big)}{2\pi i\sin2\pi(1-s)}\right)$$ $$=\frac{2\pi a^2}{\sqrt{1-(1-b)^2}}\left(\psi\big(\frac a2+s\big)-\psi\big(\frac a2+1-s\big)\right)\tag{2}$$ $$I_2(b\to0)=-\frac{4\pi a}{\sqrt{2b}}+2a^2\psi^{(1)}\big(\frac a2\big)-4+O(\sqrt b)\tag{2a}$$ Taking together (1a) and (2a) we see that the divergent terms ($\sim\frac1{\sqrt b}$) cancel, and the answer is $$\boxed{\,\,I(a)=2a^2\psi^{(1)}\big(\frac a2\big)-4a-4\,\,}$$ It is straightforward to check, using the asymptotics of $\psi^{(1)}$, that $I(a)\to 0$ at $a\to\infty$, as it should be.

Quick numeric check also confirms the answer - https://www.wolframalpha.com/input?i=16%5Cint_%7B-%5Cinfty%7D%5E%5Cinfty+%5Cfrac%7Bx%5E2%7D%7B%284x%5E2%2B2%5E2%5Cpi%5E2%29%5Csinh%5E2%28x%29%7Ddx and https://www.wolframalpha.com/input?i=8%5Cpsi1%281%29-8-4

Answer 2

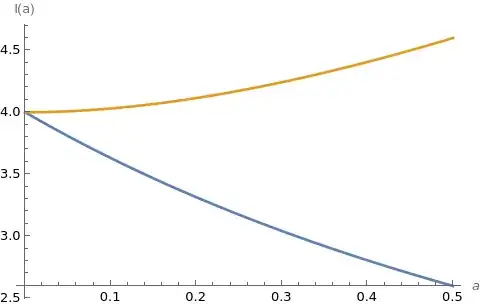
For evaluation purposes assume that $a>0$ and is not an even number.

The approach you mentioned can be used to evaluate the integral.

Integrate the function $$f(z) = 8a \, \frac{z^{2}}{4z^{2}+a^{2}\pi^{2}} \frac{1}{\sinh^{2}(z)} $$ around a rectangular contour with vertices at $z= \pm x$, $z= \pm x + i (2N+1) \pi/2$, where $x \ge 0$ and $N \in \mathbb{N}$.

Letting $x \to \infty$, the integrals along the left and right sides of the contour vanish because $\sinh(z)$ grows exponentially as $\Re(z) \to \pm \infty$.

And on the line $x + i(2N+1)\pi/2$, $x \in \mathbb{R}$, $\frac{1}{\sinh^{2}(z)} = - \frac{1}{\cosh^{2}(x)}$, which is independent of $N$.

Letting $N \to \infty$, the integral along the top of the contour goes to $$8a \int_{-\infty}^{\infty} \frac{1}{4}\frac{1}{\cosh^{2}(x)} \, \mathrm dx = 4a .$$

(The dominated convergence theorem allows us to move the limit inside the integral after we parametrize the top of the contour. )

Therefore, we have $$\int_{-\infty}^{\infty} f(x) \, \mathrm dx +4a = 2 \pi i \left(\operatorname*{Res}_{z = a \pi i /2} f(z) + \sum_{n=1}^{\infty} \operatorname*{Res}_{z=n \pi i} f(z) \right). $$

The residue at $z= a \pi i/2$ is $\frac{- a^{2} \pi i}{2 \, {\color{red}{\sin}^{2}}(\tfrac{a \pi}{2})} $.

(If $a$ is even, then the pole at $z= a \pi i /2$ is a triple pole.)

And since $$ \begin{align} f(z) &= 8a \left(\frac{n^{2}}{4n^{2}-a^{2}}+ \frac{2in a^{2}}{(4n^{2}-a^{2} ) \pi} (z-n \pi i) +O \left((z-n \pi i)^{2}\right) \right) \left(\frac{1}{(z- n \pi i)^{2}} + O(1) \right) \\ &= 8a \left(\frac{n^{2}}{4n^{2}-a^{2}} \frac{1}{(z-n \pi i)^{2}} + \frac{2na^{2}i}{(4n^{2}-a^{2})^{2} \pi } \frac{1}{z- n \pi i} + O(1)\right), \end{align}$$ it follows that $$\operatorname*{Res}_{z = n\pi i} f(z) = \frac{16n a^{3}i}{(4n^{2}-a^{2})^{2}}. $$

Using the series definition for trigamma function along with the recurrence relation for the trigamma function, we have $$ \begin{align} \sum_{n=1}^{\infty} \operatorname*{Res}_{z=\pi n i} f(z) &= 16 a^{3} i \sum_{n=1}^{\infty} \frac{n}{(4n^{2}-a^{2})^{2}} \\ &= \frac{2 a^{2}i}{\pi} \sum_{n=1}^{\infty} \left(\frac{1}{(2n-a)^{2}} - \frac{1}{(2n+a)^{2}} \right) \\ &= \frac{a^{2} i}{2\pi} \sum_{n=0}^{\infty} \left(\frac{1}{(n+1-\frac{a}{2})^{2}}- \frac{1}{(n+1+\frac{a \pi}{2})^{2}} \right) \\ &= \frac{a^{2}i}{2 \pi} \left(\psi_{1} \left(1-\frac{a}{2} \right)- \psi_{1} \left(1+ \frac{a}{2} \right) \right) \\&= \frac{a^{2}i}{2 \pi} \left(\psi_{1} \left(1- \frac{a}{2} \right)- \psi_{1} \left(\frac{a}{2} \right) + \frac{4}{a^{2}}\right), \end{align}$$ which agrees with the result from Mathematica.

Therefore, using the reflection formula for the trigamma function, we have $$ \begin{align} 8a \int_{-\infty}^{\infty} \frac{x^{2}}{4x^{2}+a^{2} \pi^{2}} \frac{1}{\sinh^{2}(x)}\, \mathrm dx &= a^{2} \psi_{1} \left(\frac{a}{2} \right) - a^{2} \psi_{1} \left(1- \frac{a}{2} \right) -4 + a^{2}\pi^{2} \csc^{2} \left(\frac{a \pi}{2} \right) -4a \\ &= 2a^{2} \psi_{1} \left(\frac{a}{2} \right) -4a -4, \end{align} $$ which agrees with Svyatoslav's result.

This result should hold even if $a$ is even.