6

On page 78 of R. Goldblatt's "Topoi: The Categorial Analysis of Logic", the author introduces the notion of an element of a category thusly: if a category $\mathcal C$ has a terminal object $\mathbf 1$, then an element of a $\mathcal C$-object $a$ is a $\mathcal C$-arrow $x:\mathbf 1\to a$. Then he goes on to define the name of a $\mathcal C$-arrow $f:a\to b$, assuming $\mathcal C$ has exponentials. Denoting by $pr_a:{\mathbf 1}\times a\to a$ the product projection, the name of $f$ is the arrow ${}^{\lceil}f^{\rceil}:{\mathbf 1}\to b^a$ that is the exponential adjoint of $f\circ pr_a$. Then ${}^{\lceil}f^{\rceil}$ is the unique arrow such that $ev\circ {}^{\lceil}f^{\rceil}\times 1_a = f\circ pr_a$. He then concludes claiming that for any $\mathcal C$-element $x:{\mathbf 1}\to a$ of $a$, $$ev \circ \langle {}^{\lceil}f^{\rceil}, x\rangle = f \circ x,$$ where $\langle {}^{\lceil}f^{\rceil}, x\rangle: {\mathbb 1}\to b^a\times a$ is the product arrow. He then immediately proposes as an exercise to "prove this last statement."

Up until this point I have been able to do this book's exercises without too much hassle, but I've been stuck on this one for 2 days now. The furthest I got is the following diagram:

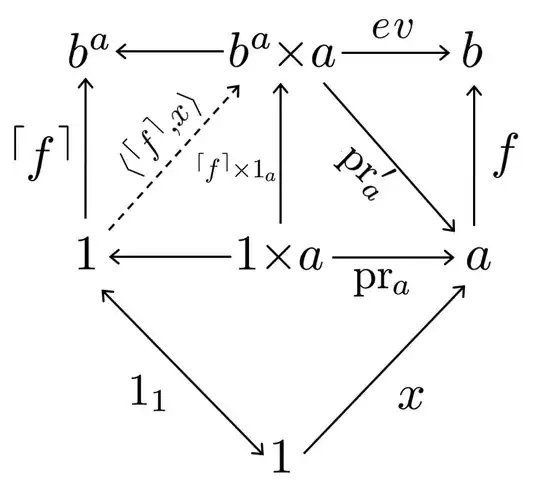
Diagram

From this I can conclude that $$pr_a' \circ \langle {}^{\lceil}f^{\rceil}, x\rangle = x \circ 1_1,$$ yielding $$f \circ pr_a' \circ \langle {}^{\lceil}f^{\rceil}, x\rangle = f \circ x.$$ The claim would follow if $ev = f \circ pr_a'$, but I can't find any reason why that upper right triangle of the diagram would commute. I'd appreciate help/suggestions. Thanks.

MJD
  • 67,568
  • 43
  • 308
  • 617
purpleflyer
  • 99
  • 4
  • 1
    That upper right triangle wouldn't commute even in $\mathsf{Set}$ -- the direct arrow would send $(g, x) \mapsto g(x)$, whereas the other composition would send $(g, x) \mapsto f(x)$, for $g : A \to B$ and $x : A$. – Daniel Schepler Nov 05 '24 at 16:56
  • 1
    As a hint, can you come up with a morphism in the other direction $1 \to 1 \times a$ of the middle left morphism in your diagram? Then, you can check whether you get a commutative triangle in the upper left of the middle diamond. – Daniel Schepler Nov 05 '24 at 17:08
  • 1
    @DanielSchepler the obvious map in the direction you indicated is $\langle 1_{\mathbf 1}, x \rangle$, and indeed chasing the product diagrams it follows that ${}^{\lceil}f^{\rceil}\times 1_a \circ \langle 1_{\mathbf 1}, x \rangle = \langle {}^{\lceil}f^{\rceil}, x \rangle$.

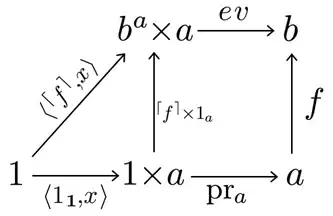
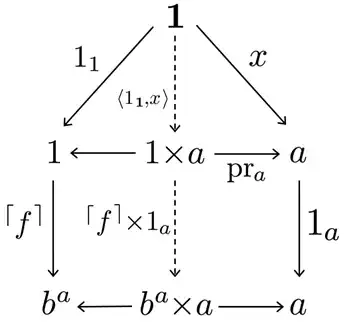
    From that the claim will follow using $pr_a \circ \langle 1_{\mathbb 1}, x \rangle = x$.

    Thanks! Whats the "proper" way to close the question? Should I reply to myself with the answer or is there a way to attribute the solution to you?

     – purpleflyer Nov 05 '24 at 20:07
  • 1
    https://math.stackexchange.com/a/3629148/104041 – Shaun Nov 15 '24 at 20:15
  • https://stackoverflowteams.com/c/topos-theory-study-group/questions – Shaun Nov 15 '24 at 20:16
  • 1
    @Shaun your second link says the Team is private, says to contact Team owner and doesn't even tell me who the owner is. – purpleflyer Nov 17 '24 at 08:26
  • 1
    Sorry about that, @purpleflyer! This is the first time I shared such a link! If you're interested in the study group, let me know; I'll try to get you in. – Shaun Nov 17 '24 at 12:28
  • 1
    @Shaun you'll need their email address, then under Admin Settings > Users & Permissions > Invite Users. – Daniel Donnelly Nov 17 '24 at 15:32
  • 1
    @Shaun wow I don't even know how I answered that before. This time around I've skipped past that particular section in the book. – Daniel Donnelly Nov 17 '24 at 15:34
  • @purpleflyer I suggest that you post a complete answer. This brings extra visibility to the solution. Also you can then accept it as well. It is good practice to include attribution yes. – Martin Brandenburg Nov 17 '24 at 15:55
  • @purpleflyer It's my free SO Teams instance. But both Shaun & I are Admins. You could ping us in Chat exchange an email then we can have you join us Remember not to put exactly your email address because of webcrawlers. – Daniel Donnelly Nov 17 '24 at 20:09

1 Answers1

1

Solution using the hint from Daniel Schepler

We wish to show that $ev\circ\langle {}^{\lceil} f^{\rceil},x\rangle = f\circ x$. From the universal property of exponentials we have $$\tag{1} f\circ pr_a = ev\circ{}^{\lceil} f^{\rceil}\times 1_a, $$ and from the property of product arrows we have $$\tag{2} pr_a\circ\langle 1_{\mathbf 1}, x\rangle = x. $$ Assume that the left triangle commutes in the following diagram (we already know the square commutes from (1)).

Diagram 1

Then we have \begin{align} ev\circ \langle {}^{\lceil}f^{\rceil}, x\rangle &= ev\circ {}^{\lceil}f^{\rceil}\times 1_a\circ\langle 1_{\mathbb f}, x\rangle \\ &=f\circ pr_a\circ\langle 1_{\mathbf 1}, x\rangle \\ &=f\circ x. \quad\quad\mbox{(using (2))} \end{align}

Thus is suffices to show that the left triangle from previous diagram commutes, i.e., to show that ${}^{\lceil}f^{\rceil}\times 1_a\circ\langle 1_{\mathbb 1}, x\rangle = \langle {}^{\lceil}f^{\rceil}, x\rangle.$

In order to do that, consider the diagram below.

Diagram 2

The diagram commutes by the definition of product and product map. Then from the uniqueness of the product arrow we have \begin{align} {}^{\lceil}f^{\rceil}\times 1_a\circ\langle 1_{\mathbf 1}, x\rangle&= \langle {}^{\lceil}f^{\rceil}\circ 1_{\mathbf 1}, 1_a\circ x\rangle \\ &= \langle {}^{\lceil}f^{\rceil}, x\rangle. \end{align}

purpleflyer
  • 99
  • 4