How to find the limit of $a_{n+2}=\frac{1}{3}(a_{n+1}+2a_n)$

Question

EDIT 1: I forgot to indicate that the initial values are: $a_0=0, a_1=1$.

I managed to prove that it is a Cauchy Sequence (later found that it was easier to prove that it is contractive), therefore, it converges to lets say $a$.

However, this leads to an identity, namely $a=\frac{1}{3}(a+2a)$.

I found some help on the site, for example here, where they mention the characteristic polynomial to find the recurrence relation.

Although the method helped me to find my limit, $a=\frac{3}{5}$, I was wondering why it works. Moreover, how can this method be applied to more complicated recurrence relations, and where is it used the most? (I recall something similar from ODEs)

Here is a plot that helped me understand the behavior of the sequence.

Thanks for any explanation.

Answer 1

As stated this is not true. Take $a_1=a_2=0$, then $a_n=0$ for all $n \in \mathbb{N}$. You need to provide what the initial values of this sequence are and from there we can work forward.

Since the question has now been edited to give the initial values, here's one way in which we can proceed.

Since we have $3 a_{n+2}=a_{n+1}+2a_{n}$, you can rewrite this to $3(a_{n+2}-a_{n+1})=2(a_{n}-a_{n+1})$. Now sum both sides from $1$ to $N-1$ to obtain $3a_{N+1}+2a_{N}=2a_1+3a_2$ which is equivalent to stating that for $n \ge 1$ we have $a_{n+1}+\frac{2}{3}a_n=\frac{1}{3}(2a_1+3a_2)$.

Now substitute $a_n=t_n+\frac{1}{5}(2a_1+3a_2)$, this will give you $t_{n+1}=\frac{-2}{3}t_n$, which is just a geometric progression. You can solve for $t_n$ and substitute back into $a_n$ to obtain $a_n=\frac{(-2)^n}{3^n} \cdot \frac{3}{5} (a_1-a_2)+\frac{1}{5}(2a_1+3a_2)$. This clearly converges to $\frac{1}{5}(2a_1+3a_2)$, now substitute your initial values to find the limit.

Also, this method easily generalizes to any recurrence of the form $a_{n+2}= \frac{1}{m+l}(ma_{n+1}+la_{n})$ where $m^2+l^2≠0$ and $m,l>0$.

Answer 2

Like second order linear differential equations, second order linear difference equations are solved by an exponential ansatz. So you assume that the solution is of the form $a_n = c \alpha^n$ and determine the values of $c$ and $\alpha$.

In your case, we have $$ 3 a_{n+2} - a_{n+1} - 2 a_n = 0 \implies c \alpha^n (3\alpha^2 - \alpha-2)=0. $$ For a nontrivial solution (depending on nontrivial initial conditions), we need $c\ne 0$, so $$ 3\alpha^2 - \alpha-2 = 0 \implies \alpha = 1\quad \text{or}\quad \alpha = -\frac23. $$ (This is where the characteristic polynomial comes from.) Therefore, a general solution is of the form $$ a_n = c_1 1^n + c_2 \left(-\frac23\right)^n. $$ We can then solve for $c_1$ and $c_2$ using the initial conditions: $$ a_0 = c_1 +c_2,\qquad a_1 = c_1 - \frac{2c_2}3. $$ In your example plot, you had $a_0 = 0$ and $a_1 = 1$, so we get $$ c_1 = -c_2 = \frac35. $$ Since $|-\frac23|<1$, we conclude that $a_n \rightarrow c_1 = \frac35$ as $n\rightarrow \infty$.

Answer 3

Let's take a general 2nd-order recurrence relation with constant coefficients without a free term: $$ a_{n+2} = ca_{n+1} + da_n $$ The following polynomial is called a characteristic polynomial of the relation: $$ x^2 - cx - d $$ The importance of such polynomial lies in the following theorem: $$ \forall x\ (x^2 - cx-d=0) \Rightarrow \forall n\ x^{n+2} = cx^{n+1} + dx^n $$ Proof: $cx^{n+1}+dx^n = x^n(cx+d) = x^nx^2 = x^{n+2}$

Thus, by solving the characteristic polynomial, you can get solutions for respective recurrence relation (if $x_1, x_2$ - roots of the polynomial, then sequences $\{x_1^n\}_n^\infty$ and $\{x_2^n\}_n^\infty$ satisfy the relation).

It is easy to show, that any linear combination of sequences, satisfying the recurrence relation, also satisfies the relation: $$ \forall a_n, b_n\ (a_{n+2} = ca_{n+1} + da_n) \wedge (b_{n+2} = cb_{n+1} + db_n) \Rightarrow \forall k, l\ ka_{n+2} + lb_{n+2} = k(ca_{n+1} + da_n) + l(cb_{n+1} + db_n) = c(ka_{n+1} + lb_{n+1}) + d(ka_n + b_n) $$
So, if $x_1$ and $x_2$ are the roots of the characteristic polynomial, then for any $k, l$ sequence $kx_1^n + lx_2^n$ satisfies the relation, but we need to find such coefficients, that the starting conditions ($a_0, a_1$) are also satisfied. You could find them by solving the following system of linear equations: $$ \cases{kx_1^0 +lx_2^0 = a_0\\kx_1^1+lx_2^1 = a_1} $$ Observe, that if $x_1$ and $x_2$ are distinct, then the system always has a unique solution, as the respective matrix is not degenerate: $$ \left|\array{x_1^0 & x_2^0\\x_1^1 & x_2^1}\right| = \left|\array{1 & 1\\x_1 & x_2}\right| = x_2 - x_1 \ne 0 $$

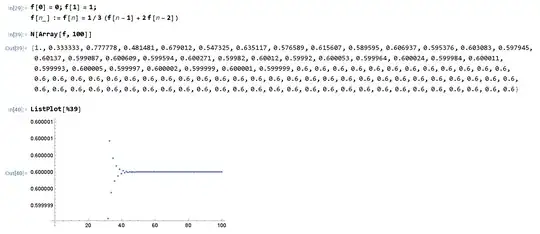
In your case, $x_1 = 1, x_2 = -\dfrac23, k = \dfrac35, l = -\dfrac35, a_n = \dfrac35\cdot1^n - \dfrac35 \cdot \left(-\dfrac23\right)^n = -\dfrac35\cdot \left(-\dfrac23\right)^n + \dfrac35, \lim_{n\to\infty}a_n = \dfrac35$.

In more general case, given a recurrence relation with constant coefficients $$ a_{n+r} = c_1a_{n+r - 1} + ... + c_ra_n $$ with characteristic polynomial $$ (x-x_1)^{p_1}\cdot...\cdot(x-x_s)^{p_s}, \sum_{i=1}^s p_i = r, x_i \text{ are distinct} $$ the following $r$ sequences satisfy the relation: $$ x_1^n,\ nx_1^n,\ n^2x_1^n,\ ...,\ n^{p_1-1}x_1^n,\ x_2^n,\ ...,\ n^{p_2-1}x_2^n,\ ...,\ x_s^n,\ ...,\ n^{p_s-1}x_s^n $$ and there is a unique linear combination of these sequences, that satisfies the relation and the starting conditions.

It is also possible to use this method, when a free term is present $$ a_{n+r} = c_1a_{n+r - 1} + ... + c_ra_n + f $$ by substituting $n$ with $n+1$ and subtracting the original relation: $$ a_{n+r} = c_1a_{n+r - 1} + ... + c_ra_n + f \Rightarrow \cases{a_{n+r} = c_1a_{n+r - 1} + ... + c_ra_n + f\\a_{n+r+1} = c_1a_{n+r} + ... + c_ra_{n+1} + f} \Rightarrow\\\Rightarrow \cases{0 = -a_{n+r}+ c_1a_{n+r - 1} + ... + c_ra_n + f\\a_{n+r+1} = c_1a_{n+r} + ... + c_ra_{n+1} + f} \Rightarrow\\\Rightarrow a_{n+r+1} = (c_1+1)a_{n+r} + (c_2-c_1)a_{n+r-1} +...+ (c_r-c_{r-1})a_{n+1} - c_ra_n $$ This way we get rid of the free term, but increase the order of the relation. To solve it with the method above, you need to update the starting conditions by calculating $a_r$.

Answer 4

Let $b_n=a_{n+1}-a_n\Rightarrow b_0=a_1-a_0=1$ $$ 3(a_{n+2}-a_{n+1})=-2(a_{n+1}-a_n)\Rightarrow $$ $$ b_{n+1}=-\frac{2}{3}b_n\Rightarrow b_{n}=\left(-\frac{2}{3}\right)^nb_0=\left(-\frac{2}{3}\right)^n\Rightarrow $$ $$ a_n=(a_n-a_{n-1})+(a_{n-1}-a_{n-2})+\ldots+(a_1-a_0)+a_0= $$ $$ =b_{n-1}+b_{n-2}+\ldots+b_0=\sum_{i=0}^{n-1}\left(-\frac{2}{3}\right)^i\Rightarrow $$ $$ \lim_{n\to\infty}a_n=\frac{1}{1+\frac{2}{3}}=\frac{3}{5} $$

Answer 5

Rearrange the equation, as follows: $$3(a_{n+2}-a_{n+1}) = 2(a_{n}-a_{n+1})$$ Let $b_{n+1}=a_{n+1}-a_{n}$. Then, $$b_{n+1}=\left(-\frac{2}{3}\right)b_{n}$$

If you sum $b_n$ you obtain: $$\sum_{k=1}^{M}{b_k}=\sum_{k=1}^{M}{a_{k}-a_{k-1}}=a_{M}-a_0$$ But, the sum $b_n$ is also a geometric series: $$\sum_{k=1}^{M}{b_k}=b_1+\left(-\frac{2}{3}\right)b_{1}+\left(-\frac{2}{3}\right)^2b_{1}+...+\left(-\frac{2}{3}\right)^{M-1}b_{1} =\frac{1-\left(-\frac{2}{3}\right)^{M}}{1-\left(-\frac{2}{3}\right)}$$

If you then take the limit: $$\lim_{M\rightarrow\infty}\sum_{k=1}^{M}{b_k}=\lim_{M\rightarrow\infty}a_{M}-a_0=\frac{1}{1-\left(-\frac{2}{3}\right)}=\frac{3}{5}$$ Since $a_0 = 0$, we conclude $$\lim_{M\rightarrow\infty}a_{M}=\frac{3}{5}.$$

Answer 6

(This probably could be done more simply, but this is off the top of my head.)

If $a(n+1) =ra(n)+(1-r)a(n-1) $ then, if $a(n0-1)$ and $a(n0)$ are the initial values for $a(...)$,

$\begin{array}\\ a(n+1)-a(n) &=ra(n)+(1-r)a(n-1)-a(n)\\ &=(r-1)a(n)+(1-r)a(n-1)\\ &=(1-r)(a(n-1)-a(n))\\ \text{so}\\ a(m)-a(n0) &=\sum_{n=n0}^{m-1}(a(n+1)-a(n))\\ &=\sum_{n=n0}^{m-1}((1-r)(a(n-1)-a(n)))\\ &=(1-r)(a(n0-1)-a(m-1)\\ \text{so}\\ a(m) &=(r-1)a(m-1)+a(n0)+(1-r)a(n0-1)\\ &=ba(m-1)+c \qquad b=r-1, c=a(n0)+(1-r)a(n0-1)\\ \text{so}\\ \dfrac{a(m)}{b^m} &=\dfrac{ba(m-1)+c}{b^m}\\ &=\dfrac{a(m-1)}{b^{m-1}}+\dfrac{c}{b^m}\\ \text{so}&\text{letting } u(m)=\dfrac{a(m)}{b^m}\\ u(m) &=u(m-1)+\dfrac{c}{b^m}\\ \text{so}\\ u(m)-u(m-1) &=\dfrac{c}{b^m}\\ \text{so}\\ u(n)-u(n0) &=\sum_{m=n0+1}^n(u(m)-u(m-1))\\ &=\sum_{m=n0+1}^n\dfrac{c}{b^m}\\ &=\dfrac{c (b^{-n} - b^{-n0})}{1 - b}\\ \text{so}\\ \dfrac{a(n)}{b^n} &=\dfrac{a(n0)}{b^{n0}}+\dfrac{c (b^{-n} - b^{-n0})}{1 - b}\\ \text{or}\\ a(n) &=a(n0)b^{n-n0}+\dfrac{c (1 - b^{n-n0})}{1 - b}\\ &=a(n0)b^{n-n0}+\dfrac{c }{1 - b}-\dfrac{c b^{n-n0}}{1 - b}\\ &=a(n0)(r-1)^{n-n0}+\dfrac{c }{2-r}-\dfrac{c (r-1)^{n-n0}}{2-r}\\ \end{array} $

If $|r-1| < 1$ then $a(n) \to \dfrac{c }{2-r} =\dfrac{a(n0)+(1-r)a(n0-1)}{2-r} $.

Given $n0=1, a(n0)=1, a(n0-1)=0$, have $r=\frac13, c =a(n0)+(1-r)a(n0-1) =1 $, $\dfrac{c}{2-r} =\dfrac{1}{2-\frac13} =\dfrac35 $.