4

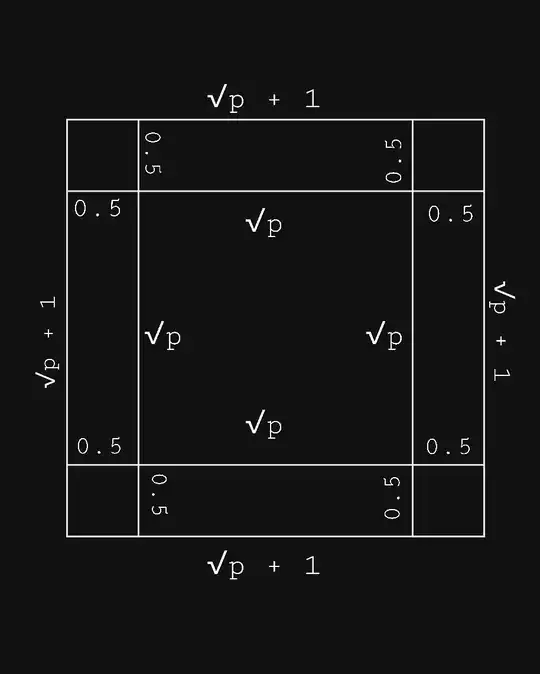
I came up with a formula for finding the next perfect square with a given square. The formula is written as follows:

$$y = p + \left(1 + 2\sqrt{p}\right)$$

where $p$ is the given square or past result.

This can also be put as

$$y_n = y_{n-1} + \left(1 + 2\sqrt{y_{n-1}}\right)$$

If you put in the number $9$, it shows up as this:

$$\begin{align} y &= 9 + \left(1 + 2\sqrt{9}\right)\\[4pt] y &= 16 \end{align}$$

Every number I plugged in gave me the next square, and even with decimals, it gave me a correct answer. This left me wondering if it will always work.

I would also like to ask if it already exists. I looked up this formula, but I didn’t find it anywhere, so I’m not sure if someone already came up with it.

Blue
  • 83,939
Ayden Hannan
  • 43
  • 11
    Hint: substitute $p = n^2$. – mihaild Oct 24 '24 at 12:48
  • 2
    Welcome to Math.SE! ... By the earlier comment, $p=n^2$ gets you to $y=(n+1)^2$ pretty quickly. This is a straightforward application of the relation $(a+b)^2=a^2+2ab+b^2$, and as such is already known to mathematics. ... Importantly, this does not diminish the significance of the fact that you found something that wasn't already known to you. Congratulations on your discovery! Keep it up. – Blue Oct 24 '24 at 14:06
  • @Blue Thanks! Also, thanks for making my explanation more clear, I wasn’t sure how to put it. I’m in high school pre-calc, so I probably should know this, but I’m glad that you explained it. – Ayden Hannan Oct 24 '24 at 14:17
  • 2
    You remind me of myself when I was younger: I was also playing around, trying to find formulae. I "invented" the formula for the sum of the angles of a polygon: $(180-\frac{360}{n}) \times n$, which I later realised was simply equal to $(n-2) \times 180$. This did not discourage me and I later also "invented" Pascal's triangle, Fermat's small hypothesis and a "simple" way to divide by $5.8$, which gave me one of the proudest looks I ever received from my father :-) Keep going! – Dominique Oct 24 '24 at 14:20
  • 2
    @AydenHannan: You're welcome! ... Don't get discouraged if (when!) someone has thought of a result before you. Steve Fisk called this an Accident of Time, and we all encounter it regularly. Just keep in mind that there are a lot of smart and ridiculously-prolific mathematicians ahead of us on the timeline. (Euler, I'm looking at you!) Even so, they cannot have thought of everything, so we all still have a shot. :) ... BTW: I, too, was a high school pre-calc student when I started seeing math as a creative art. (See my note here.) Cheers! – Blue Oct 24 '24 at 14:51

2 Answers2

3

Your formula is in fact equal to:

$$(n+1)^2 = n^2+2n+1$$

(Just replace $y$ by $(n+1)^2$ (the next square) and $p$ by $n^2$ (the square you start from.)

Dominique
  • 3,267
1

enter image descriptio here

Here is a visual representation of how your formula works

Gwen
  • 3,910
  • 6
  • 19