1

I want to know the reasoning why the auxiliary function is in such form.

A couple examples:

On the OpenStax website there is a Calculus Volume 2 book. The proof of Taylor's theorem with remainder in Lagrange form can be found here: Chapter 6.3, Theorem 6.7. The auxiliary function used there is as follows:

$$ \ g(t) = f(x) - f(t) - f'(t)(x - t) - \frac{f''(t)}{2!}(x - t)^2 - \cdots - \frac{f^{(n)}(t)}{n!}(x - t)^n - R_n(x)\frac{(x - t)^{n+1}}{(x - a)^{n+1}}. \ $$

We are fixing $x$ here, right? And as I understand it, the $\frac{(x - t)^{n+1}}{(x - a)^{n+1}}$ part scales the $R_n(x)$ error term as $t$ changes. But why don't we fix $t$? I mean, we are expanding the Taylor series around $t$, so why should $t$ change? It doesn't make sense to me. I see that when $t = x$, the error term vanishes, and when $t = a$, we get the single $R_n(x)$ term. But isn't the point around which we are performing the expansion supposed to be fixed?

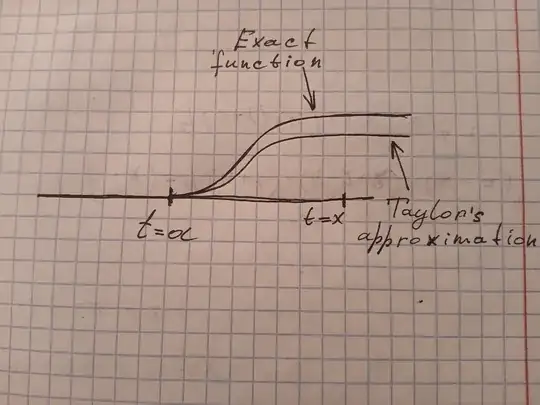
I also tried sketching it:

enter image description here

and I don't understand why the error term should vanish at $t = x$, because the divergence there should be significant. And at $t = a$ there is no error at all.

Principles of Mathematical Analysis by Walter Rudin p.111. The auxiliary function $g(t)$ looks like this:

enter image description here

In Rudin's book, he introduced an error term as "M(t - b)^n", which is not an obvious move at all, and the best "justification" I've seen is "this term is carefully chosen". And all I can think is "oh, carefully chosen, really?".

For example proof of Lagrange's Mean Value Theorem uses auxiliary function:

$$ F(x) = f(x) - \left[ \frac{f(b) - f(a)}{b - a} (x - a) + f(a) \right] $$

But it didn't come out of nowhere. The point is that to construct this function, we subtract from some function $f(x)$, the secant passing through two points on $f(x)$ and since they are equal at two points, their difference is zero at these two points. That's it, you can use Rolle's theorem. However, I did not come to it myself, but watched a video lesson.

And there is no magic. Whereas in the OpenStax Calculus book, the auxiliary function for Taylor's theorem proof, looks like it's pulled from a hat.

I have absolutely no idea what hat and what magic these functions were pulled out of.

No matter what article, video lecture, or book I find, nowhere does it explain where this function comes from. I want to understand the reasoning that could lead to this function. Without any reasoning, the appearance of this function seems like this: "A mathematician was sitting, handwaving and thinking, and suddenly decided that they wanted the function to be like this, and voilà, this function suddenly worked".

It even seems that those who learn math are either not expected to understand this detail, or the author of the article or video lecture doesn't know where it came from and just borrowed a "classical proof" to use in their material.

The proofs themselves (the ones mentioned above) weren't very hard to understand, but this particular gap makes any proof feel "artificial". I'm learning math on my own in my spare time (I don't have access to a teacher or professor), using open resources. However, I haven't been able to find any justification or "proof" for these functions, which has led to frustration.

Maybe there really isn't supposed to be a proof for them? How do mathematicians come up with such "functions pulled from a hat"?

Michael
  • 93
  • On Rudin's text, $g$ is defined so that the proof becomes a proof about the zeroes of $g$ and of its derivatives. This is fairly common since the proof will then rely on theorems that were previously proven. You'll get used to this sort of procedure and it isn't uncommon for a proof to feel artificial at first. – Silver M. Golden Oct 20 '24 at 18:50
  • @Useless But how to build this bridge from "getting used" to "artificiality" of proof and auxiliary function to actually understanding with what thoughts the auxiliary function was built? For example, in Rudin's function he introduced an error term as "M(t - a)^n", which is not an obvious move at all, and the best "justification" I've seen is "this term is carefully chosen". And all I can think is "oh, carefully chosen, really?". – Michael Oct 20 '24 at 23:49
  • Did you check Keith Conrad notes at https://kconrad.math.uconn.edu/blurbs/analysis/TaylorRemainder.pdf ? – Paramanand Singh Oct 26 '24 at 04:54
  • @ParamanandSingh I see he wrote "argument is based on a comment by Pieter-Jan De Smet on the page" (and what this comment actually saying is "it's clear that there is M such that M(b-a)^(n+1)") and then he introduced the auxiliary function using some C (like in the comment) like this $E(x) = ... + \frac{C}{(n+1)!} (b - x)^{n+1}$. This is still function "pulled from hat". I mean, author kind of saying that he already know from somewhere that the remainder should look like this. – Michael Oct 26 '24 at 05:37
  • It's pretty the same approach as in Rudin's book I've mentioned above. All these proofs aren't hard to understand, really, but they are assume that the part that begins the proof is self-evident (I mean aux functions) and does not require explanation. These both in my question. – Michael Oct 26 '24 at 05:49
  • Well considering the Taylor series upto n terms with last term being $f^{(n)}(a) (x-a) ^n/n! $ it is natural to expect that next term should be $f^{(n+1)}(a)(x-a)^{n+1}/(n+1)!$ and therefore we want the remainder to look something almost like the next term. Don't you think it is natural to expect so? – Paramanand Singh Oct 26 '24 at 09:55
  • Once we guess the form of remainder it is not so difficult to get to the auxiliary function. – Paramanand Singh Oct 26 '24 at 09:57
  • @ParamanandSingh yes, it's pretty natural reasoning. But we are still saying that "we know something about remainder before proof of it". I'm not a professional mathematician (it's obvious, of course) so I want to ask, is this approach really valid? – Michael Oct 26 '24 at 12:19
  • @ParamanandSingh what about a function from OpenStax? I've also seen an opinion that a mathematician could actually try dozens of auxiliary functions before he found one that really worked and just used it in the proof. But I can't understand why there's no any explanation. Because the term $R_n(x)\frac{(x - t)^{n+1}}{(x - a)^{n+1}}$ doesn't look natural. – Michael Oct 26 '24 at 12:23
  • @Michael you ask whether a way to try to solve problems is "really valid". Mathematicians do not do all their scratch work using strict logic. They play around with various ideas, sometimes based on guesses or intuition. The role of experience can't be ignored. What seems what like an unmotivated step to one person can seem natural to another. In this case, we hope the remainder has a certain appearance and play around to make that work out. You see in writing only the end result. Try cases with small $n$. – KCd Oct 26 '24 at 14:56
  • Taylor series derivation – Felix Marin Oct 26 '24 at 16:47

2 Answers2

1

If you want another way to obtain the remainder let's consider $$S(t)=f(x)-\sum_{k=0}^{n} \frac{f^{(k)}(t) \cdot (x-t)^k}{k!}$$ so $$S'(t)=-\sum_{k=0}^{n} \frac{f^{(k+1)}(t) \cdot (x-t)^k}{k!}-\frac{f^{(k)}(t) \cdot (x-t)^{k-1}}{k-1!}$$ in this case we consider when $$k=0,(x-t)^{k-1}=0 \quad\text{because of the first term of the Taylor expansion} \quad f(t)(x-t)^{0}$$

$$S'(t)=-\sum_{k=0}^{n} \frac{f^{(k+1)}(t) \cdot (x-t)^k}{k!}+\sum_{k=1}^{n}\frac{f^{(k)}(t) \cdot (x-t)^{k-1}}{k-1!}$$ so $$S'(t)=\frac{f^{(n+1)}(t)\cdot(x-t)^{n}}{n!}$$ Now, this looks like more to the Lagrange form of the remainder. We can try to use the mean value theorem: $$\frac{S(x)-S(t)}{x-t}=-\frac{f^{(n+1)}(\xi)\cdot(x-\xi)^{n}}{n!}$$ $$\xi, \text{is in between of x and t}$$ So if we want to get rid of the term $$(x-\xi)^{n}$$ consider $$ g(t)=(x-t)^{n+1}$$ By the Cauchy mean value theorem: $$\frac{S(x)-S(t)}{g(x)-g(t)}=\frac{S'(\xi)}{g'(\xi)}=-\frac{f^{(n+1)}(\xi)\cdot(x-\xi)^{n}}{-n!(n+1)\cdot (x-\xi)^{n} }=\frac{f^{(n+1)}(\xi)}{n+1!}$$ $$\xi, \text{is in between of x and t}$$ We know that $$S(x)=0, g(x)=0$$ $$S(t)=\frac{f^{(n+1)}(\xi)}{n+1!}\cdot(x-t)^{n+1}\quad \text{We need now to fix t, that is the point we are evaluating the function }$$ $$R(x)=\frac{f^{(n+1)}(\xi)}{n+1!}\cdot(x-x_0)^{n+1}$$

aaaa
  • 11
  • I just noticed that you considered t as the variable in the taylor expansion but I choosed x, oops – aaaa Oct 29 '24 at 21:47
0

The reason to introduce a function of $t$, which evaluates an error term between $a$ and $x$, is to enable the use of Rolle's theorem. The latter defines an intermediate value $c$ where the derivative vanishes, corresponding to a maximum. This allows to find an upper bound on the remainder of the limited Taylor development.