Unexpected and Interesting Applications of the $n^\text{th}$ Roots of Unity

Question

$\textbf{1.}$ I was recently looking at a trigonometry textbook for revision and I found that the identities

$$\cos x+\cos\left(x+\frac{2\pi}3\right)+\cos\left(x+\frac{4\pi}3\right)=0$$ $$\sin x+\sin\left(x+\frac{2\pi}3\right)+\sin\left(x+\frac{4\pi}3\right)=0$$

can be very quickly proved using complex numbers by taking the real and the imaginary parts of:

$$e^{ix}(1+\omega+\omega^2)=0$$

where $\omega=e^{2\pi i/3}$, apart from the standard formulae for $\sum_{k=0}^n\sin(\alpha+k\beta)$ and $\sum_{k=0}^n\cos(\alpha+k\beta)$. I found this use of the cube roots of unity quite intriguing and found that this can be generalized as:

$$\sum_{k=0}^{n-1}\cos\left(x+\frac{2k\pi}{n}\right)=\sum_{k=0}^{n-1}\sin\left(x+\frac{2k\pi}{n}\right)=0$$

---

$\textbf{2.}$ In destructive interference of $n$ plane harmonic waves with the same amplitude, if the waves are considered in the order at which each wave reaches a fixed point in space, the phase difference between $2$ consecutive waves must be $\Delta\varphi=\frac{2\pi}{n}$. This is a consequence of the fact that the $n^{\text{th}}$ roots of unity are symmetrically distributed in the complex plane, since

$$\sum_{k=0}^{n-1}\text{cis}\left(\frac{2k\pi}{n}\right)=0$$ where $\text{cis}\theta=e^{i\theta}$.

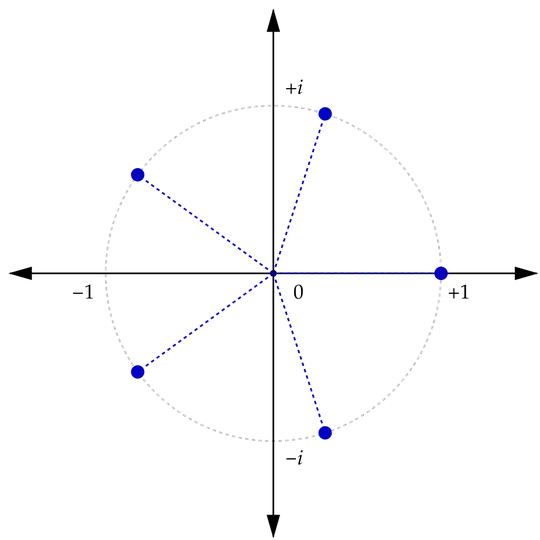
For example, when $n=5$:

---

$\textbf{3.}$ The general solution of the differential equation $$\frac{\mathrm d^ny}{\mathrm dx^n}=y$$ is $$y=\sum_{k=1}^{n}C_ke^{\text{cis}\left(\frac{2k\pi}{n}\right)x}$$

where $C_1, C_2,\cdots C_n$ are arbitrary constants.

I find this particularly interesting since apparently at the first glance, the ODE seems to have nothing to do with the roots of unity.

This can be proved by letting $y=e^{rx}$ which yields the result $r^n=1$, from which it is imminent for the $n^{\text{th}}$ roots of unity to appear in the general solution.

---

Are there any other interesting uses of the $n^\text{th}$ roots of unity?

Answer 1

Let $p=2n+1$ be a prime, and consider the $2^n$ expressions $$ \pm1\pm2\pm3\dotsb\pm n $$ For each $r$, $r=0,1,2,\dotsc,p-1$, how many of these expressions evaluate to a number that leaves a remainder $r$ when you divide by $p$?

E.g., take $p=7$, so $n=3$, and we are looking at the eight expressions $$ \pm1\pm2\pm3 $$ two of which ($1+2-3$, and $-1-2+3$) evaluate to zero, the others evaluate to $6,2,4,-4,-2,-6$, which on division by $7$ give the remainders $1,2,3,4,5,6$ once each (though not in that order).

For every $p$, the answer is that the nonzero remainders all arise the same number of times, and the zero remainder arises once more or once less than the nonzero remainders, depending on the remainder when you divide $p$ by $8$.

One way to prove this is to let $\theta=e^{2\pi i/p}$ and then work with $$ (\theta+\theta^{-1})(\theta^2+\theta^{-2})\times\dotsb\times(\theta^n+\theta^{-n}) $$ and show that it equals $\sum_{r=0}^{p-1}N(r)\theta^r$ where $N(r)$ is the number of expressions leaving remainder $r$ on division by $p$. [There's a little more to it than that, but that's a big piece of the solution.]

There's a generalization of this question, where you take a prime $p=ef+1$, look at the multiplicative group of the integers modulo $p$, which is a cyclic group of order $ef$, take the subgroup $C$ of order $f$, and ask how many ways there are of getting a particular value $r$ modulo $p$ by adding together elements, one from each coset of $C$. The original problem is the case $f=2$, and the approach to the general problem also involves the roots of unity of order $p$.

Answer 2

$n^{th}$ roots of unity can surprisingly be used to compute sums and products involving binomial coefficients, for example consider the sum, $${n \choose 0} + {n \choose 3} + {n \choose 6} + \cdots$$ To compute this sum consider the binomial expasion of $(1+x)^{n}$ $$(1+x)^{n} = {n \choose 0}x^{0} + {n \choose 1}x^{1} + \cdots + {n \choose n}x^{n}$$ plug in $x = 1,\omega,\omega^2$, where $1, \omega, \omega^2$ are the cube roots of unity $$2^n = {n \choose 0} + {n \choose 1} + \cdots $$ $$(1+\omega)^n = {n \choose 0} + {n \choose 1}\omega + {n \choose 2}\omega^2 + {n \choose 3} + \cdots + {n \choose 6} + \cdots$$ $$(1+\omega^2)^n = {n \choose 0} + {n \choose 1}\omega^2 + {n \choose 2}\omega^4 + {n \choose 3} + \cdots + {n \choose 6} + \cdots$$

Adding all these three expressions we get, $$2^n + (1+\omega)^n + (1+\omega^2)^n = 3\Bigg({n \choose 0} + {n \choose 3} + {n \choose 6} + \cdots\Bigg)$$ Now $$2^n + (1+\omega)^n + (1+\omega^2)^n = 2^n + 2\text{Re}((1+\omega)^n)$$ $$ = 2^n + 2\cos\frac{n\pi}{3}$$ Which is obtained using the De Moivre's theorem, thus we have, $$\boxed{{n \choose 0} + {n \choose 3} + {n \choose 6} + \cdots = \frac{1}{3}\Bigg(2^n + 2\cos\frac{n\pi}{3}\Bigg)}$$ Which is quite an interesting result as one would not imagine a relation between binomial coefficients and the cosine function!

Answer 3

To complement the differential equation example, a similar thing happens for the difference equation (or, recurrence relation) $u_{n+k}=u_n$, where $k$ is fixed, and $n=0,1,2,\dotsc$. The general solution is a linear combination of $n$th powers of $k$th roots of unity.

Answer 4

Roots of unity can be used to prove many trigonometric identities and to calculate many special or exact trigonometric values.

As an example let us find $x= \cos 36^\circ.$ Take the root of unity $w=e^{\frac{\pi i}5}$ which satisfies the equations $w^5=-1$ and $w^4-w^3+w^2-w+1=0.$ $$x=\frac{w+w^{-1}}2=\frac{w-w^4}2\tag1$$ $$x^2=\frac{w^2-2w^5+w^8}4=\frac{w^2+2-w^3}4\tag2$$ From $(1)$ and $(2)$, $4x^2-2x-1=0$ and thus $x=\frac{\sqrt5+1}4=\frac\phi 2$ is half of the golden ratio.

Systematic way of making these computations is through the Chebyshev Polynomials.

Answer 5

Conway and Jones, Trigonometric diophantine equations, Acta Arithmetica XXX (1976) 229-240, available at http://matwbn.icm.edu.pl/ksiazki/aa/aa30/aa3033.pdf study equations such as $$ A\cos2\pi a+B\cos2\pi b+C\cos2\pi c+D\cos2\pi d=E $$ with all variables rational by turning them into vanishing sums of roots of unity (indeed, the subtitle of the paper is, "On vanishing sums of roots of unity"). The methods have been applied to finding all rational solutions of $$ \sin\pi x\sin\pi y\sin\pi z\sin\pi w=t $$ and of $$ \sin\pi x\sin\pi y=\sin\pi z\sin\pi w $$ and the masterful work, Poonen and Rubinstein, The number of intersection points made by the diagonals of a regular polygon, SIAM J. Discret. Math. 11 (1995) 135-156.

Answer 6

One particular problem which involved roots of unity was this;

(it was unexpectedly used after a lot of effort being put into just realizing the generating function)

Let $X = \{1,2,\ldots,2000\}$. How many subsets $T$ of $X$ are such that the sum of the elements of $T$ is divisible by 5?

Here's the solution

This problem does not seem to utilize roots of unity until it's properties are realized to make working with the generating function a lot simpler. The roots of unity can be used to solve complex discrete counting problems involving generating functions and cyclic permutations.

Answer 7

In Field Theory, the proof that a polynomial equation is solvable in radicals if and only if its Galois group is a solvable group depends heavily on the properties of field extensions containing particular roots of unity.