Definition of limit in terms of only delta.

Question

When introduced to limits in school, we are told that the limit of a function $f(x)$ as $x$ tends to $x_0$, if it exists, is a specific value that the function tends towards as $x$ tends to a specific value, $x_0$, from the right and from the left. This is accompanied by examples where we put really close values to $x_0$ into our calculator and convince ourselves that the function really does tend to this value from both sides.

In college, we are then told that this can be formalised using the $\epsilon$-$\delta$ definition, with little reference to what was previously known about them. The college definition starts by defining $\epsilon$, which bounds the outputs of a function within an interval about the limit. The outputs of the function should not go beyond this first bound. Then it goes on to say that there is some $\delta$, which bounds the arguments of the function within an interval about $x_0$. The inputs of the function should not go beyond this second bound. It then goes on to say that the outputs for this second bound should lie within the interval of the allowable outputs of the first bound.

The first approach is to get close to $x_0$ and see if the outputs get close to some value we call the limit. The second approach is to bound the outputs and say we can always bound the inputs so that their output is within the originally set bounds for the output.

Why do we abandon the school version? Is the school version even able to be formalised? If it can be, why is this formalisation not shown; is there any relationship between the two perspectives, and are they even different perspectives?

What follows is my attempt at answering the second question: formalising the school version.

The version taught in school starts with some very small $\delta>0$. You put that into your calculator, get an even smaller $\delta>0$, put that into your calculator, and you can see the function approximating some value. So, we are analysing $f(x\pm \delta)$. We can put conditions on the function based on whether the monotonicity of the function is increasing, decreasing or just constant from the left or right. This is based on the observation that if we were to plot inputs against outputs, from our calculations, we would hope to see a curve or line that gets close to or is a limit.

In other words, we are analysing the function to see if it behaves a certain way for small values of $\delta$. To get a limit, you don't concern yourself with how the function looks beyond this small $\delta$ but within this small $\delta$. And within this small $\delta$, the function must behave a certain way. So the choice of $\delta$ depends on the function behaving a certain way. If we have that the function behaves a certain way around the value we want to approach, then we can find the limit. If we can't find a region where the function behaves a certain way, then we can't find the limit. Now, this certain way is where the function from both the left and right is increasing, decreasing or constant. And so we need to know what inputs about $x_0$ on either side give unique monotonicities in $f(x)$.

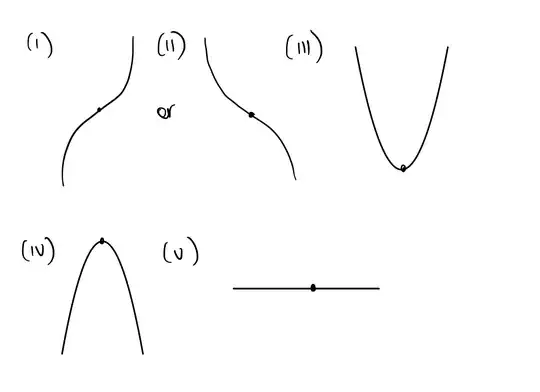
The limit $\lim_{x \rightarrow x_0}f(x)$ is the unique value that satisfies the following conditions, which are that for every $\delta > 0$, $$\ \left|\lim_{x \rightarrow x_0}f(x) \right|< f(x_0 \pm \delta) \tag {I}$$ or $$\ \left|\lim_{x \rightarrow x_0}f(x) \right|> f(x_0 \pm \delta) \tag{II}$$ or $$\ 2\lim_{x \rightarrow x_0}f(x)-f(x_0 - \delta) < \lim_{x \rightarrow x_0}f(x) < f(x_0 + \delta) \tag{III}$$ or $$\ 2\lim_{x \rightarrow x_0}f(x)-f(x_0 - \delta) > \lim_{x \rightarrow x_0}f(x) > f(x_0 + \delta) \tag{IV}$$ or $$\ f(x_0 - \delta)=\lim_{x \rightarrow x_0}f(x)=f(x_0 + \delta). \tag{V}$$

The graphs correspond to the cases I am considering for the limit definition, with $x$-$y$ axis treated as usual. For $(\text{III})$ and $(\text{IV})$, I flipped the half of the function left of the limit so they would be in the form for cases $(\text{I})$ and $(\text{II})$.

Thanks!

Edit: I somehow missed the questions directly similar to mine. Links: Does the epsilon-delta definition of limits truly capture our intuitive understanding of limits?, specifically this answer on Math SE is helpful if it is true. This answer seems related to non-standard analysis here.

Answer 1

I think the two versions are exactly the same.

The first version says "as $x$ gets close to $x_0$, $f(x)$ gets close to $L$, and we can get $f(x)$ as close to $L$ as we like by picking values of $x$ very close to $x_0$". The problem with this is we haven't defined what the heck "gets close to" means nor what exactly we mean by "as". This is way too informal to analytically mean anything.

The delta epsilon defines those issues explicitly. "$f(x)$ gets as close to $L$ as we like" means that for any measurable value, we may find values of $x$ so that $f(x)$ is within that distance to $L$. And "by picking values of $x$ very close to $x_0$" means that to get $f(x)$ within or first distance of $L$, we select values of $x$ within a small enough distance of $x_0$.

And the distance we want to get $f(x)$ within $L$ of... is designated as $\epsilon$ (we don't "define" $\epsilon$; we indicate the concept of arbitrary nearness between $f(x)$ and $L$ as being an arbitrarily small positive value $\epsilon$). And the distances between $x$ and $x_0$ that we must pick from to get $f(x)$ that close to $L$ is designated as $\delta$.

Thus, the two concepts are exactly the same. But one is colloquially ill-defined "well, you know what we mean obviously" unusable common language. And the other is logically precise and, more importantly, capable of being quantitatively applied.

......

I think the biggest confusion students have is when we say "as $x$ gets close to $x_0$, $f(x)$ gets close to $L$" is that intuitive it seems that $|x-x_0| < \delta$ is of primary importance and $|f(x)-L|<\epsilon$ is the consequence. But when we do the delta-epsilon we have $\epsilon$ be the premise and $\delta$ the dependent result.

But if you reread "As $x$ gets close to $x_0$, $f(x)$ gets close to $L$" has its important emphasis on "we can't get $f(x)$ as close to $L$ as we like" and it's only after we "set a goal for ourselves" of just how close we want $f(x)$ to get to $L$ that we declare "to do that we have $x$ within so and so of $x_0$"

After all, consider $f(x) = (x-2)^2+5$, and we consider that as $x$ gets closer and closer to $2$, we have $f(x)$ getting closer and closer to ... $4$. See if $x=1$ or $x=3$ we have $f(x)=6$. That is $2$ away from $4$. And if $x=1.5$ or $x=2.5$ we have $f(x)=5.25$ and that is $1.25$ away from $4$. That's closer. And if $x=1.9$ or $x=1.9$, we have $f(x)=5.01$, and that is $1.01$ away from $4$. Closer still! And if $x=1.9999$ or $x=2.0001$, we have $f(x)=5.00000001$, and that is $1.00000001$ from $4$, and that's closer still. We just get closer and closer.

But that's not what we want. We never get closer than $1$. And we want to get as "as close as we want". $\lim_{x\to 2} (x-2)^2 + 5 = 5$, and we do that by saying "if we want to get within $1$ of $5$, we take $x$ within $1$ of $2$. And if we want to get within $0.25$, we take $x$ within $0.5$. And if we want to get within $0.01$, we take $x$ within $0.1$ of $2$. And so on".

And so... The driving force is to get $f(x)$ "as close as we like" to $x$ (that is $\epsilon$) and "we do that by taking $x$ close to $x_0$" (that is $\delta$) is dependent.

===

Here's an example

Take $f(x) = x^3 - 11.8499875x^2 + 46.774901875x - 61.4998078125$.

And consider $\lim_{x\to 4} f(x)$.

We might notice that as we punch numbers closer and closer to $4$, we get values closer and closer to $0$.

If $x=3.5$, $f(x)= -0.074998125$
If $x=3.75$, $f(x)=0$
If $x=3.9$, $f(x)=0.002999625$
If $x=3.99$, $f(x) = 0.00026367$
If $x=3.999$, $f(x) = 0.0000248346375$

That is close enough to your calculator to conclude $\lim_{x\to 4}f(x) = 0$.

But notice two things:

1. "As $x$ gets closer to $4$, $f(x)$ gets closer to $0$" is not true. Ans $x$ goes for $3.75$ to $3.9$, $f(x)$ actually gets further away from $0$.

And

2. How do we know it will continue to get close to $0$? What if there's some lower point that $f(x)$ never gets closer than?

Indeed, as $f(4)$ is actually calculatable, it's reasonable that $\lim_{x\to 4} f(x)$ ought to be the same thing as $f(4)$, shouldn't it? Is $f(4)$ actually equal to $0$?

No. If $x=4$, then $f(x) = -0.0000003125$

Tricked you! $\lim_{x\to 4} f(x)$ is actually equal to $-0.0000003125$ and not $0$ after all.

The thing is we need some way to say "getting within $0.00000003125$ is not actually good enough; we need to get much closer than that; we need to get within a billionth, or a trillionth, or a googolth".

Any definition where you concentrate on $x$ getting close to $x_0$ rather without setting a goal as to actually how close we want $f(x)$ to get to $L$ is DOOMED to fail.

And to set that goal as to actually how close we want $f(x)$ to get to $L$ first.... well, that is the delta-epsilon definition.

Now, in case you are curious about who I made up that $f(x)$ just for the purpose of tricking you:

I set up $f(x) = (x-3.75)(x-4.1)(x-3.9999875)=x^3 - 11.8499875x^2 + 46.774901875x - 61.4998078125$. Here, roots are all fairly close to $x=4$. But I wanted there to be points where $f(x)$ actually pulls away from our goal. If I had do $f(x) = (x-10)(x+15)(x-3.9999875)$, that would happen when $x$ passes from a root ($10$ or $-15$) to another. If the roots were far apart, that wouldn't be an issue, but $3.75$ and $4.1$ are close enough to $4$ that it could occur in our testing. But the main thing is the actual root we are aiming for when we go for $x=3.9, x=3.99$ and $x=3.999$ is not $4$ but $3.9999875$. If we had continued to go further, we might have found that we start getting away from zero as we try $x=3.99999, x=3.999999, x=3.999999999$ and so on. But if we don't know how close we need to get, we can't gauge if we are close enough. That's (again) why we have to start with a goal of $f(x)$ is as close as we want to $L$ and not "start with $x$ close to $x_0$ and keep going closer until $f(x)$ and $L$ are 'close enough'". What does the fudge cycle "close enough" mean? We HAVE to resolve that first.

Answer 2

To answer the general differences between the two versions, I'll see if there is an equivalence between them when a limit exists.

$\epsilon$-$\delta$ definition $\Leftarrow$ school definition?

Call the left end point $x_0$-$δ_0$ and the right end point $x_0$+$δ_1$, within which the function is either increasing, decreasing or constant. If we put these points into the function and get the minimum distance between these outputs and the limit, and let $\epsilon$ be that point. We can see that there is by definition $\delta>0$ equal to the endpoint whose output is the minimum of the two. If we then let $\epsilon$ be less than the endpoint whose output is the minimum distance, there will be the desired $\delta>0$, because the function will have an inverse within the region it is increasing or decreasing. And where it is a region that is constant equal to the limit that distance from the limit will necessarily be 0 which will be less than any $\epsilon$ so the $\delta$ can be any point within the endpoints of a constant region.

$\epsilon$-$\delta$ definition $\Rightarrow$ school definition?

epsilon-delta does not imply that for any function with a limit at a point there is some $\delta$ for which the function has a continuous line or curve connected to the limit.

Assume that there is some $\delta$. Then look at the lines $x=x_0\pm$$\delta/2$. The function could be within $\epsilon$ distance of the limit but connect to the maximum allowable $\epsilon$ then come from the least allowable $\epsilon$ from bottom and continue. And so there does not have to be some $\delta$. The function could be discontinuous like this ad infinitum never connecting to the limit while still eventually taking its value.

The connection I see is that if you draw a continuous line or curve connecting the points for each output $\delta>0$ to each other and to the limit then this line should be continuous for any function. But with the school definition, as I’ve laid it out, you only define limits that have continuity whereas the $\epsilon$-$\delta$ defines limits no matter how the function looks about the exact limit. The function just has to converge to the limit even if it is discontinuous between points. The school definition then covers a straightforward subset of all possible functions and since elementary functions in school were continuous there was no need to introduce the more broad $\epsilon$-$\delta$ definition that doesn't require some continuity about the limit.